
【题目】(1)计算:(﹣1)3+|﹣6|×2﹣1﹣![]() ;
;
(2)解不等式:x![]() <
<![]() ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
科目:初中数学 来源: 题型:
【题目】点C、D在线段AB上,若点C是线段AD的中点,2BD>AD,则下列结论正确的是( ).
A. CD<AD- BD B. AB>2BD C. BD>AD D. BC>AD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直线l经过点A(﹣2,0)和点B(0,1),点M在x轴上,过点M作x轴的垂线交直线l于点C,若OM=2OA,则经过点C的反比例函数表达式为( )
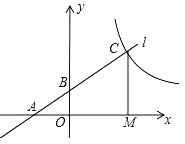
A.y=![]() B.y=
B.y=![]() C.y=
C.y=![]() D.y=
D.y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第24届冬奥会将于2022年在北京和张家口举行,冬奥会的项目有滑雪(如高山滑雪、单板滑雪等),滑冰(如速度滑冰、花样滑冰等),冰球,冰壶等.如图,有4张形状、大小、质地均相同的卡片,正面分别印有单板滑雪、速度滑冰、冰球、冰壶4种不同的图案,背面完全相同.现将这4张卡片洗匀后正面向下放在桌子上.

(1)从中随机抽取1张,抽出的卡片上恰好是滑雪项目图案的概率是 .
(2)若印有单板滑雪、速度滑冰、冰球、冰壶4种不同图案的卡片分别用A,B,C,D表示,从中随机抽取两张,试用画树状图或列表的方法求出印有冰球图案的卡片被抽中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在矩形ABCD中,AD=nAB,点M,P分别在边AB,AD上(均不与端点重合),且AP=nAM,以AP和AM为邻边作矩形AMNP,连接AN,CN.
(问题发现)
(1)如图(2),当n=1时,BM与PD的数量关系为 ,CN与PD的数量关系为 .
(类比探究)
(2)如图(3),当n=2时,矩形AMNP绕点A顺时针旋转,连接PD,则CN与PD之间的数量关系是否发生变化?若不变,请就图(3)给出证明;若变化,请写出数量关系,并就图(3)说明理由.
(拓展延伸)
(3)在(2)的条件下,已知AD=4,AP=2,当矩形AMVP旋转至C,N,M三点共线时,请直接写出线段CN的长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:当点P在射线OA上时,把![]() 的的值叫做点P在射线OA上的射影值;当点P不在射线OA上时,把射线OA上与点P最近点的射影值,叫做点P在射线OA上的射影值.
的的值叫做点P在射线OA上的射影值;当点P不在射线OA上时,把射线OA上与点P最近点的射影值,叫做点P在射线OA上的射影值.
例如:如图1,△OAB三个顶点均在格点上,BP是OA边上的高,则点P和点B在射线OA上的射影值均为![]() =
=![]() .
.

(1)在△OAB中,
①点B在射线OA上的射影值小于1时,则△OAB是锐角三角形;
②点B在射线OA上的射影值等于1时,则△OAB是直角三角形;
③点B在射线OA上的射影值大于1时,则△OAB是钝角三角形.
其中真命题有 .
A.①②B.①③C.②③D.①②③
(2)已知:点C是射线OA上一点,CA=OA=1,以〇为圆心,OA为半径画圆,点B是⊙O上任意点.
①如图2,若点B在射线OA上的射影值为![]() .求证:直线BC是⊙O的切线;
.求证:直线BC是⊙O的切线;
②如图3,已知D为线段BC的中点,设点D在射线OA上的射影值为x,点D在射线OB上的射影值为y,直接写出y与x之间的函数关系式为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强每天坚持引体向上锻炼,他记录了某一周每天做引体向上的个数,如下表:
星期 | 日 | 一 | 二 | 三 | 四 | 五 | 六 |
个数 | 11 | 12 | 13 | 12 |
其中有三天的个数墨汁覆盖了,但小强己经计算出这组数据唯一众数是13,平均数是12,那么这组数据的方差是( )
A.![]() B.
B.![]() C.1D.
C.1D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB//CD,点E是直线AB上的点,过点E的直线l交直线CD于点F,EG平分∠BEF交CD于点G.在直线l绕点E旋转的过程中,图中∠1,∠2的度数可以分别是( )
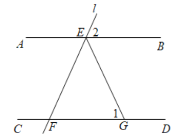
A.30°,110°B.56°,70°C.70°,40°D.100°,40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是AB上一点,连接DE.过点A作AF⊥DE,垂足为F,⊙O经过点C、D、F,与AD相交于点G.
(1)求证:△AFG∽△DFC;
(2)若正方形ABCD的边长为4,AE=1,求⊙O的半径.
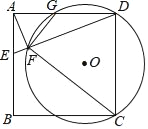
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com