


 ……………………………2分
……………………………2分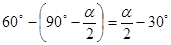
 即α=2β+60° ………………………………7分
即α=2β+60° ………………………………7分 ………………………8分
………………………8分
 ……………………………… 9分
……………………………… 9分 (0≤x<2)………………10分
(0≤x<2)………………10分

 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 为
为 ,运动时间为
,运动时间为 ,则下列图形能大致地刻画
,则下列图形能大致地刻画 与
与 之间关系的是( )
之间关系的是( )
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (年)逐年成直线上升,y与
(年)逐年成直线上升,y与
 之间的关系式;
之间的关系式;
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 、
、 两地相距10千米,甲班从
两地相距10千米,甲班从 地出发匀速步行到
地出发匀速步行到 地,乙班从
地,乙班从 地出发匀速步行到
地出发匀速步行到 地.两班同时出发,相向而行.设步行时间为
地.两班同时出发,相向而行.设步行时间为 小时,甲、乙两班离
小时,甲、乙两班离 地的距离分别为
地的距离分别为 千米、
千米、 千米,
千米, 、
、 与
与 的函数关系图象如图所示,根据图象解答下列问题:
的函数关系图象如图所示,根据图象解答下列问题: 、
、 与
与 的函数关系式;
的函数关系式; 地多少千米?
地多少千米?
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 与时间
与时间 之间函数关系的是
之间函数关系的是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com