
 如图,双曲线y1=$\frac{{k}_{1}}{x}$(x<0)经过A(-2,3),双曲线y2=$\frac{{k}_{2}}{x}$(x2>0)经过C点,D点在y轴正半轴上,B(1,0)点在x轴的正半轴上,若四边形ABCD是矩形.
如图,双曲线y1=$\frac{{k}_{1}}{x}$(x<0)经过A(-2,3),双曲线y2=$\frac{{k}_{2}}{x}$(x2>0)经过C点,D点在y轴正半轴上,B(1,0)点在x轴的正半轴上,若四边形ABCD是矩形.分析 (1)根据待定系数法即可求得;
(2)根据平行线的性质求得OF=1,进而求得△BOF是等腰直角三角形,从而求得△AGD是等腰直角三角形,进一步求得△ADG≌△BCH,即可求得C坐标,然后根据待定系数法即可求得双曲线y2(x>0)解析式.
解答  解:(1)∵双曲线y1=$\frac{{k}_{1}}{x}$(x<0)经过A(-2,3),
解:(1)∵双曲线y1=$\frac{{k}_{1}}{x}$(x<0)经过A(-2,3),
∴k1=-2×3=-6,
∴y1=-$\frac{6}{x}$(x<0);
(2)设AB与y轴的交点为F,作AE∥y轴,交x轴于E,作AG∥x轴,交y轴于G,
∴$\frac{OF}{AE}$=$\frac{OB}{EB}$,
∵A(-2,3),B(1,0),
∴AE=OG=3,OE=AG=2,OB=1,
∴$\frac{OF}{3}$=$\frac{1}{1+2}$,
∴OF=1,
∴OF=OB,
∴∠OFB=45°,
∴∠AFD=45°,
∵∠BAD=90°,
∴∠ADO=45°,
∴AG=2,
∴DG=AG=2,
∵∠ABO=45°,∠ABC=90°,
∴∠CBH=45°,
∴△BCH是以BC为斜边的等腰直角三角形,
∵AD=BC,
∴△ADG≌△BCH,
∴BH=AG=GH=DG=2,
∴C(3,2),
∵双曲线y2=$\frac{{k}_{2}}{x}$(x2>0)经过C点,
∴k2=2×3=6,
∴y2=$\frac{6}{x}$(x>0).
点评 本题考查了待定系数法求反比例函数的解析式以及矩形的性质,求得C点的坐标是解题的关键.


 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:选择题
| A. | -$\sqrt{49}$=-7 | B. | $\sqrt{49}$=±7 | C. | -$\sqrt{49}$=±7 | D. | ±$\sqrt{49}$=7 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,数轴上A、B所对应的数分别为-5、10,O为原点,点P以每秒2个单位长度,点Q以每秒3个单位长度,分别自A、B两点同时出发,在数轴上运动,设运动时间为t秒,若点P、Q相向而行且OP=OQ,求t值.
如图,数轴上A、B所对应的数分别为-5、10,O为原点,点P以每秒2个单位长度,点Q以每秒3个单位长度,分别自A、B两点同时出发,在数轴上运动,设运动时间为t秒,若点P、Q相向而行且OP=OQ,求t值.查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省盐城市盐都区西片七年级下学期第一次月考数学试卷(解析版) 题型:解答题
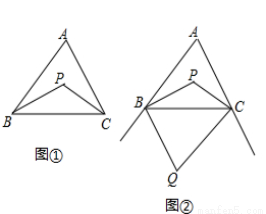
如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.
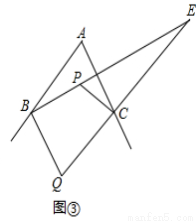
(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省盐城市盐都区西片七年级下学期第一次月考数学试卷(解析版) 题型:填空题
若△ABC中,∠A:∠B:∠C=2:3:4,则△ABC是 三角形.(填:锐角或直角或钝角)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com