
【题目】定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.
请解决下列问题:
(1)已知点M,N是线段AB的勾股分割点,且BN>MN>AM.若AM=2,MN=3,求BN的长;
(2)如图2,若点F、M、N、G分别是AB、AD、AE、AC边上的中点,点D,E是线段BC的勾股分割点,且EC>DE>BD,求证:点M,N是线段FG的勾股分割点.

【答案】(1)![]() (2)证明见解析.
(2)证明见解析.
【解析】试题分析:(1)①当MN为最大线段时,由勾股定理求出BN;②当BN为最大线段时,由勾股定理求出BN即可;
(2)先证出点M、N分别是AD、AE的中点,得出BD=2FM,DE=2MN,EC=2NG,求出EC2=BD2+DE2,得出NG2=FM2+MN2,即可得出结论
试题解析:(1)∵点M,N是线段AB的勾股分割点,且BN>MN>AM, AM=2,MN=3
∴![]()
![]()
∴BN=![]()
(2)证明 ∵点F、M、N、G分别是AB、AD、AE、AC边上的中点
∴FM、MN、NG分别是△ABD、△ADE、△AEC的中位线
∴BD=2FM,DE=2MN,EC=2NG
∵点D,E是线段BC的勾股分割点,且EC>DE>BD
∴![]()
∴![]()
∴![]()
∴点M,N是线段FG的勾股分割点


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=BD;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下问题,不适合用普查的是( )
A. 了解全班同学每周阅读的时间B. 亚航客机飞行前的安全检测
C. 了解全市中小学生每天的零花钱D. 某企业招聘部门经理,对应聘人员面试
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我省2014年的快递业务量为1.4亿件,受益于电子商务发展和法治环境改善等多重因素,快递业务迅猛发展, 2016年的快递业务量达到4.5亿件.设2015年与2016年这两年的平均增长率为x,则下列方程正确的是( )
A. 1.4(1+x)=4.5 B. 1.4(1+2x)=4.5
C. 1.4(1+x)2=4.5 D. 1.4(1+x)+1.4(1+x)2=4.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,
且∠ABM=∠BAM,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下调查中适合做普查的是( )
A. 值日老师调查各班学生的出勤情况 B. 调查长江水的污染情况
C. 调查某种钢笔的使用情况 D. 中央电视台调查某节目的收视率
查看答案和解析>>
科目:初中数学 来源: 题型:
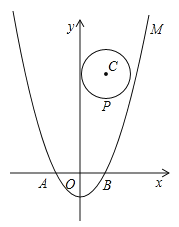
【题目】如图,在平面直角坐标系xOy中,将二次函数![]() 的图象M沿x轴翻折,把所得到的图象向右平移2个单位长度后再向上平移8个单位长度,得到二次函数图象N.
的图象M沿x轴翻折,把所得到的图象向右平移2个单位长度后再向上平移8个单位长度,得到二次函数图象N.
(1)求N的函数表达式;
(2)设点P(m,n)是以点C(1,4)为圆心、1为半径的圆上一动点,二次函数的图象M与x轴相交于两点A、B,求![]() 的最大值;
的最大值;
(3)若一个点的横坐标与纵坐标均为整数,则该点称为整点.求M与N所围成封闭图形内(包括边界)整点的个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com