


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:阅读理解
| a2+b2 |
| b2+c2 |
| c2+a2 |
| 2 |
 +b+c的正方形来研究.
+b+c的正方形来研究.| a2+b2 |
| b2+c 2 |
| a2+c2 |
| a2+b2 |
| b2+c2 |
| c2+a2 |
| 2 |
| x2+4 |
| y2+9 |
| a2+b2 |
| 4a2+b2 |
| a2+4b2 |
查看答案和解析>>
科目:初中数学 来源:2012-2013学年上海市静安杨浦等六区初三一模(期末)数学试卷(解析版) 题型:填空题
在边长为6的正方形中间挖去一个边长为x(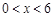 )的小正方形,如果设剩余部分的面积为y,那么y关于x的函数解析式为 .
)的小正方形,如果设剩余部分的面积为y,那么y关于x的函数解析式为 .
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(山东枣庄卷)数学(解析版) 题型:选择题
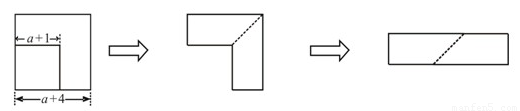
如图,从边长为(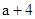 )cm的正方形纸片中剪去一个边长为(
)cm的正方形纸片中剪去一个边长为(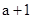 )cm的正方形(
)cm的正方形(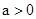 ),剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的面积为【 】
),剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的面积为【 】
A.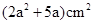 B.
B.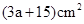 C.
C.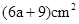 D.
D.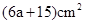
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com