
已知AB是⊙O的直径,弦CD⊥AB于点G,E是直线AB上一动点(不与点A、B、G重合),直线DE交⊙O于点F,直线CF交直线AB于点P.设⊙O的半径为R.

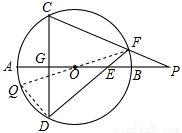
(1)如图1,当点E在直径AB上时,试证明:OE·OP=R2.(提示:作直径FQ交⊙O于Q,并连结DQ)
(2)当点E在AB(或BA)的延长线上时,以如图2点E的位置为例,请你画出符合题意的图形,标注上字母,(1)中的结论是否成立?请说明理由.
(1)连接FO并延长交⊙O于Q,连接DQ
∵FQ是⊙O直径
∴∠FDQ=90°
∴∠QFD+∠Q=90°
∵CD⊥AB
∴∠P+∠C=90°
∵∠Q=∠C
∴∠QFD=∠P
∵∠FOE=∠POF
∴△FOE∽△POF
∴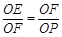
∴OE·OP=OF2=R2;
(2)成立
【解析】
试题分析:(1)连接FO并延长交⊙O于Q,连接DQ.先根据同角的余角相等得到∠QFD=∠P,再结合公共角即可证明△FOE∽△POF,然后根据相似三角形的性质即可得到结果;
(2)依题意画出图形,连接FO并延长交⊙O于M,连接CM.根据圆周角定理及等角的余角相等可得∠CFM=∠E,再结合公共角即可证明△FOE∽△POF,然后根据相似三角形的性质即可得到结果.
(1)连接FO并延长交⊙O于Q,连接DQ.

∵FQ是⊙O直径
∴∠FDQ=90°
∴∠QFD+∠Q=90°
∵CD⊥AB
∴∠P+∠C=90°
∵∠Q=∠C
∴∠QFD=∠P
∵∠FOE=∠POF
∴△FOE∽△POF
∴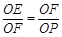
∴OE·OP=OF2=R2;
(2)如图,依题意画出图形,连接FO并延长交⊙O于M,连接CM

∵FM是⊙O直径
∴∠FCM=90°
∴∠M+∠CFM=90°
∵CD⊥AB
∴∠E+∠D=90°
∵∠M=∠D
∴∠CFM=∠E
∵∠POF=∠FOE
∴△POF∽△FOE
∴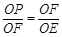
∴OE·OP=OF2=R2.
考点:本题考查的是相似三角形的性质与判定、垂径定理,圆周角定理
点评:解答本题的关键是熟练掌握直径所对的圆周角是直角;同角或等角的余角相等;同时熟记相似三角形的性质:相似三角形的对应边成比例,同时注意对应字母写在对应位置上.


科目:初中数学 来源: 题型:
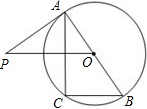 如图,已知AB是⊙O的直径,过点O作弦BC的平行线,交过点A的切线AP于点P,连接AC.
如图,已知AB是⊙O的直径,过点O作弦BC的平行线,交过点A的切线AP于点P,连接AC.| 7 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 | AB |
查看答案和解析>>
科目:初中数学 来源: 题型:
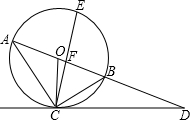
 如图,已知AB是⊙O的直径,AD切⊙O于点A,
如图,已知AB是⊙O的直径,AD切⊙O于点A, |
| EC |
 |
| CB |
| 1 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com