
【题目】如图,在ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.
(1)求证:△ABE≌△CDF;
(2)若AB=DB,猜想:四边形DFBE是什么特殊的四边形?并说明理由.

【答案】(1)证明见解析; (2)四边形DFBE是矩形,理由见解析.
【解析】证明:(1)∵四边形ABCD是平行四边形
AB=CD,∠A=∠C.
AB∥CD,∴∠ABD=∠CDB.
∵BE平分∠ABD,DF平分∠CDB,
∴∠ABE=∠ABD,∠CDF=∠CDB.
∴∠ABE=∠CDF.
在△ABE和△CDF中,
∵∠A=∠C,AB=CD,∠ABE=∠CDF,
∴△ABE≌△CDF.
(2)答:四边形DFBE是矩形。理由如下:
∵AB=DB,BE平分∠ABD
∴BE⊥AD,即∠DEB=90°.
∵AB=DB,AB=CD,∴DB=CD.
∵DF平分∠CDB,∴DF⊥BC,即∠BFD=90°.
在□ABCD中,∵AD∥BC,∴∠EDF+∠DEB=180°.∴∠EDF=90°.
∴∠DEB=∠BFD=∠EDF=90°.
∴四边形DFBE是矩形


科目:初中数学 来源: 题型:
【题目】我市某超市举行店庆活动,对甲、乙两种商品实行打折销售。打折前,购买3件甲商品和1件乙商品需用190元;购买2件甲商品和3件乙商品需用220元。而店庆期间,购买10件甲商品和10件乙商品仅需735元,这比不打折少花多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的社会实践活动中,甲、乙两人参加了射击比赛,每人射击七次,命中的环数如表:
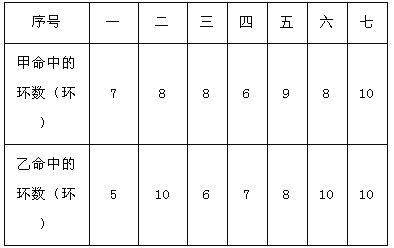
根据以上信息,解决以下问题:
(1)写出甲、乙两人命中环数的众数;
(2)已知通过计算器求得![]() =8,
=8,![]() ≈1.43,试比较甲、乙两人谁的成绩更稳定?
≈1.43,试比较甲、乙两人谁的成绩更稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是等边三角形,O为△ABC的三条中线的交点,△ABC以O为旋转中心,按顺时针方向至少旋转( )才能与原来的三角形重合.
A. 30° B. 60° C. 90° D. 120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用计算器验证,下列不等式中成立的是( )
A.sin37°24′>cos37°24′+cos3°10′
B.cos45°32′>sin45°﹣sin1°12′
C.sin63°47′<cos18°21′﹣cos87°
D.2sin30°12′<sin60°24′
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是9×7的正方形点阵,其水平方向和竖起直方向的两格点间的长度都为1个单位,以这些点为顶点的三角形称为格点三角形.请通过画图分析、探究回答下列问题:

(1)请在图中画出以AB为边且面积为2的一个网格三角形;
(2)任取该网格中能与A、B构成三角形的一点M,求以A、B、M为顶点的三角形的面积为2的概率;
(3)任取该网格中能与A、B构成三角形的一点M,求以A、B、M为顶点的三角形为直角三角形的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com