
 如图,正方形ABCD的对角线交于点O,点E是线段0D上一点,连接EC,作BF⊥CE于点F,交0C于点G.若AB=4,BF是∠DBC的角平分线,则OE的长为4-2$\sqrt{2}$.
如图,正方形ABCD的对角线交于点O,点E是线段0D上一点,连接EC,作BF⊥CE于点F,交0C于点G.若AB=4,BF是∠DBC的角平分线,则OE的长为4-2$\sqrt{2}$. 分析 利用BF是∠DBC的角平分线求得∠EBF=∠CBF,结合BF=BF,∠BFE=∠BFC=90°,可证明△BEF≌△BCF(ASA),所以BE=BC=4,根据Rt△BOC中对应的比例关系和三角函数可求得BO=2$\sqrt{2}$,所以OE=BE-BO=4-2$\sqrt{2}$.根据△BOG≌△COE可知OG=OE=4-2$\sqrt{2}$.
解答 解:∵BF是∠DBC的角平分线,
∴∠EBF=∠CBF,
∵BF⊥CE,
∴∠BFE=∠BFC=90°,
在△BEF和△BCF中,
$\left\{\begin{array}{l}{∠EBF=∠CBF}\\{BF=BF}\\{∠BFE=∠BFC}\end{array}\right.$,
∴△BEF≌△BCF(ASA),
∴BE=BC=4,
∵在Rt△BOC中,cos∠OBC=$\frac{BO}{BC}$,
即cos45°=$\frac{BO}{BC}$,
∴BO=BC•cos45°=2$\sqrt{2}$,
∴OE=BE-BO=4-2$\sqrt{2}$,
故答案为:4-2$\sqrt{2}$.
点评 主要考查了正方形的性质和全等三角形的判定.要掌握正方形中一些特殊的性质:四边相等,四角相等,对角线相等且互相平分.可利用这些等量关系求得三角形全等是解题的关键.


科目:初中数学 来源:2016-2017学年江苏省七年级下学期第一次课堂调研数学试卷(解析版) 题型:解答题
直线MN与直线PQ垂直相交于O,点A在直线PQ上运动,点B在直线MN上运动.
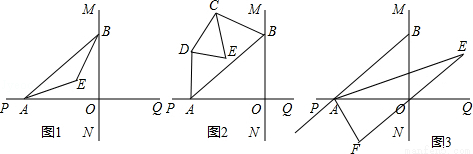
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.
(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F,在△AEF中,如果有一个角是另一个角的3倍,试求∠ABO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
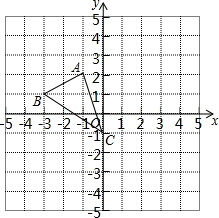 如图,图形中每一小格正方形的边长为1,已知△ABC
如图,图形中每一小格正方形的边长为1,已知△ABC查看答案和解析>>
科目:初中数学 来源: 题型:解答题
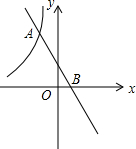 如图,一次函数y2=-2x+b(b为常数)的图象与反比例函数y1=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A,B两点,且点A的坐标为(-1,4).当y1<y2时,求x的取值范围.
如图,一次函数y2=-2x+b(b为常数)的图象与反比例函数y1=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A,B两点,且点A的坐标为(-1,4).当y1<y2时,求x的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
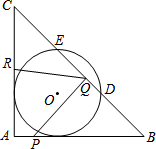 如图,在△ABC中,∠A=90°,AB=AC=12cm,半径为4cm的⊙O与AB、AC两边都相切,与BC交于点D、E.点P从点A出发,沿着边AB向终点B运动,点Q从点B出发,沿着边BC向终点C运动,点R从点C出发,沿着边CA向终点A运动.已知点P、Q、R同时出发,运动速度分别是1cm/s、xcm/s、1.5cm/s,运动时间为ts.
如图,在△ABC中,∠A=90°,AB=AC=12cm,半径为4cm的⊙O与AB、AC两边都相切,与BC交于点D、E.点P从点A出发,沿着边AB向终点B运动,点Q从点B出发,沿着边BC向终点C运动,点R从点C出发,沿着边CA向终点A运动.已知点P、Q、R同时出发,运动速度分别是1cm/s、xcm/s、1.5cm/s,运动时间为ts.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com