
【题目】如图,点A(1,6)和点M(m,n)都在反比例函数y= ![]() (x>0)的图象上,
(x>0)的图象上,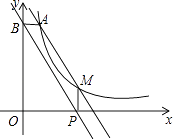
(1)k的值为;
(2)当m=3,求直线AM的解析式;
(3)当m>1时,过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,试判断直线BP与直线AM的位置关系,并说明理由.
【答案】
(1)6
(2)
解:将x=3代入反比例解析式y= ![]() 得:y=2,即M(3,2),
得:y=2,即M(3,2),
设直线AM解析式为y=ax+b,
把A与M代入得: ![]() ,
,
解得:a=﹣2,b=8,
∴直线AM解析式为y=﹣2x+8;
(3)
解:直线BP与直线AM的位置关系为平行,理由为:
当m>1时,过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,
∵A(1,6),M(m,n),且mn=6,即n= ![]() ,
,
∴B(0,6),P(m,0),
∴k直线AM= ![]() =
= ![]() =
= ![]() =﹣
=﹣ ![]() =﹣
=﹣ ![]() ,
,
k直线BP= ![]() =﹣
=﹣ ![]() ,
,
即k直线AM=k直线BP,
则BP∥AM.

【解析】解:(1)将A(1,6)代入反比例解析式得:k=6;
所以答案是:6;
【考点精析】通过灵活运用反比例函数的概念和反比例函数的图象,掌握形如y=k/x(k为常数,k≠0)的函数称为反比例函数.自变量x的取值范围是x不等于0的一切实数,函数的取值范围也是一切非零实数;反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点即可以解答此题.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=18,BC=12,正方形DEFG的顶点E,F在△ABC内,顶点D,G分别在AB,AC上,AD=AG,DG=6,则点F到BC的距离为( ) 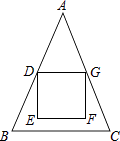
A.1
B.2
C.12 ![]() ﹣6
﹣6
D.6 ![]() ﹣6
﹣6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+bx+c,其图象抛物线交x轴于点A(1,0),B(3,0),交y轴于点C,直线l过点C,且交抛物线于另一点E(点E不与点A、B重合).
(1)求此二次函数关系式;
(2)若直线l1经过抛物线顶点D,交x轴于点F,且l1∥l,则以点C、D、E、F为顶点的四边形能否为平行四边形?若能,求出点E的坐标;若不能,请说明理由.
(3)若过点A作AG⊥x轴,交直线l于点G,连接OG、BE,试证明OG∥BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为了解员工对“六五”普法知识的知晓情况,从本公司随机选取40名员工进行普法知识考查,对考查成绩进行统计(成绩均为整数,满分100分),并依据统计数据绘制了如下尚不完整的统计表.解答下列问题:
组别 | 分数段/分 | 频数/人数 | 频率 |
1 | 50.5~60.5 | 2 | a |
2 | 60.5~70.5 | 6 | 0.15 |
3 | 70.5~80.5 | b | c |
4 | 80.5~90.5 | 12 | 0.30 |
5 | 90.5~100.5 | 6 | 0.15 |
合计 | 40 | 1.00 | |
(1)表中a= , b= , c=;
(2)请补全频数分布直方图;
(3)该公司共有员工3000人,若考查成绩80分以上(不含80分)为优秀,试估计该公司员工“六五”普法知识知晓程度达到优秀的人数. 
查看答案和解析>>
科目:初中数学 来源: 题型:
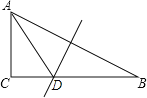
【题目】如图,Rt△ABC中,∠C=90°,BC=15,斜边AB的垂直平分线与∠CAB的平分线都交BC于D点,则点D到斜边AB的距离为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学举办运动会,在1500米的项目中,参赛选手在200米的环形跑道上进行,如图记录了跑得最快的一位选手与最慢的一位选手的跑步全过程(两人都跑完了全程),其中x代表的是最快的选手全程的跑步时间,y代表的是这两位选手之间的距离,下列说不合理的是( )
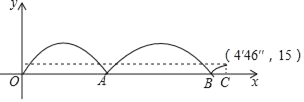
A. 出发后最快的选手与最慢的选手相遇了两次
B. 出发后最快的选手与最慢的选手第一次相遇比第二次相遇的用时短
C. 最快的选手到达终点时,最慢的选手还有415米未跑
D. 跑的最慢的选手用时4′46″
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠ABC=90°,AB=BC,D为斜边AC延长线上一点,过D点作BC的垂线交其延长线于点E,在AB的延长线上取一点F,使得BF=CE,连接EF.
(1)若AB=2,BF=3,求AD的长度;
(2)G为AC中点,连接GF,求证:∠AFG+∠BEF=∠GFE.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com