
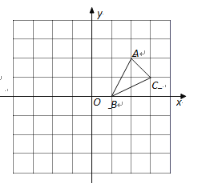
【题目】如图,△ABC的顶点的坐标分别为A(2,2),B(1,0),C(3,1)
(1)画出△ABC关于x轴对称的![]() ;
;
(2)画出△ABC绕原点O逆时针旋转90°的△A2B1C2,写出点C2的坐标;
(3)在(1)(2)的基础上,图中的![]() ,
,![]() 关于哪个点中心对称.
关于哪个点中心对称.
 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:
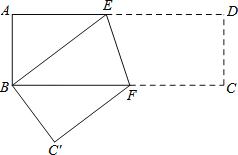
【题目】如图,在矩形纸片ABCD中,AB=4cm,AD=8cm,按如图方式折叠,使点D与点B重合,折痕为EF,则tan∠BEF=( )
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
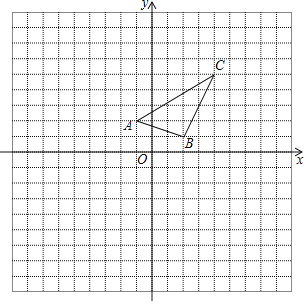
【题目】如图,在边长为1的正方形网格中建立平面直角坐标系,已知△ABC三个顶点分别为A(﹣1,2)、B(2,1)、C(4,5).
(1)以原点O为位似中心,在x轴的上方画出△A1B1C1,使△A1B1C1与△ABC位似,且相似比为2;
(2)△A1B1C1的面积是 平方单位.
(3)点P(a,b)为△ABC内一点,则在△A1B1C1内的对应点P’的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
概念理解:将△ABC 绕点 A 按逆时针方向旋转,旋转角记为 θ(0°≤θ≤90°),并使各边长变为原来的 n 倍,得到△AB′C′,如图,我们将这种变换记为[θ,n],![]() :
:![]() .
.

问题解决:(2)如图,在△ABC 中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得到△AB′C′,使点 B,C,C′在同一直线上,且四边形 ABB′C′为矩形,求 θ 和 n 的值.

拓广探索:(3)在△ABC 中,∠BAC=45°,∠ACB=90°,对△ABC作变换 得到△AB′C′,则四边形 ABB′C′为正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
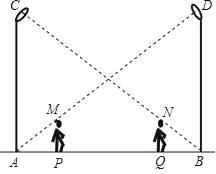
【题目】如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是_____m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=90°,A是∠MON内部的一点,过点A作AB⊥ON,垂足为点B,AB=3厘米,OB=4厘米,动点E,F同时从O点出发,点E以1.5厘米/秒的速度沿ON方向运动,点F以2厘米/秒的速度沿OM方向运动,EF与OA交于点C,连接AE,当点E到达点B时,点F随之停止运动.设运动时间为t秒(t>0).

(1)当t=1秒时,△EOF与△ABO是否相似?请说明理由;
(2)在运动过程中,不论t取何值时,总有EF⊥OA.为什么?
(3)连接AF,在运动过程中,是否存在某一时刻t,使得S△AEF=![]() S四边形AEOF?若存在,请求出此时t的值;若不存在,请说明理由.
S四边形AEOF?若存在,请求出此时t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在![]() 中,
中,![]() ,点
,点![]() 分别是边
分别是边![]() 的中点,连接
的中点,连接![]() .
.

(1)如图①,求![]() 的值;
的值;
(2)将![]() 绕点
绕点![]() 顺时针旋转到如图(2)的位置时,
顺时针旋转到如图(2)的位置时,![]() 的大小是否发生变化,若不变化,请说明理由;若发生变化,请求出它的值;
的大小是否发生变化,若不变化,请说明理由;若发生变化,请求出它的值;
(3)将![]() 绕点
绕点![]() 顺时针旋转到直线
顺时针旋转到直线![]() 的下方,且
的下方,且![]() 在同一直线上时,如图(3),求线段
在同一直线上时,如图(3),求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一场篮球比赛中,一名球员在关键时刻投出一球,已知球出手时离地面高2米,与篮圈中心的水平距离为7米,当球出手后水平距离为4米时到达最大高度4米,已知篮球运行的轨迹为抛物线,篮圈中心距离地面3.19米.
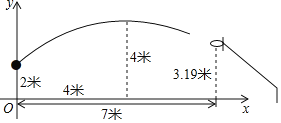
(1)以地面为x轴,篮球出手时垂直地面所在直线为y轴建立平面直角坐标系,求篮球运行的抛物线轨迹的解析式;
(2)通过计算,判断这个球员能否投中?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com