
【题目】若两个一次函数的图像与![]() 轴交于同一点,则称这两个函数为一对“
轴交于同一点,则称这两个函数为一对“![]() 牵手函数”,这个交点为“
牵手函数”,这个交点为“![]() 牵手点”.
牵手点”.
(1)一次函数![]() 与
与![]() 轴的交点坐标为________;一次函数
轴的交点坐标为________;一次函数![]() 与一次函数
与一次函数![]() 为一对“
为一对“![]() 牵手函数”,则
牵手函数”,则![]() ________;
________;
(2)请写出以![]() 为“
为“![]() 牵手点”的一对“
牵手点”的一对“![]() 牵手函数”;
牵手函数”;
(3)已知一对“![]() 牵手函数”:
牵手函数”:![]() 与
与![]() ,其中
,其中![]() ,
,![]() 为一元二次方程
为一元二次方程![]() 的两根,求它们的“
的两根,求它们的“![]() 牵手点”.
牵手点”.
【答案】(1)(-1,0),-2;(2)答案不为一,例:![]() 与
与![]() ;(3)“
;(3)“![]() 牵手点”为
牵手点”为![]() 或
或![]()
【解析】
(1)令y=0,求出x=1,可得交点坐标为(1,0),再代入y=ax+2求出a的值即可;
(2)此题答案不唯一,能写出满足条件的函数关系式即可;
(3)根据“![]() 牵手函数”的定义得
牵手函数”的定义得![]() ,整理为a+b=0,再根据
,整理为a+b=0,再根据![]() ,
,![]() 为一元二次方程
为一元二次方程![]() 的两根,求出a,b的值即可解决问题.
的两根,求出a,b的值即可解决问题.
(1)令y=0,
∴x-1=0,
∴x=1,
∴一次函数![]() 与
与![]() 轴的交点坐标为(1,0)
轴的交点坐标为(1,0)
把(1,0)代入![]() 得,
得,
a+2=0,
∴a=-2;
(2)答案不为一,例:![]() 与
与![]()
(3)![]() 与
与![]() 为一对“
为一对“![]() 牵手函数”
牵手函数”
![]() ,
,![]() .
.
![]() ,
,![]() 为
为![]() 的两根
的两根
![]() ,
,![]() ,
,![]() ,
,![]() .
.
①若![]() ,
,![]() 则
则![]() 与
与![]() 的“
的“![]() 牵手点”为
牵手点”为![]()
②若![]() ,
,![]() 则
则![]() 与
与![]() 的“
的“![]() 牵手点”为
牵手点”为![]()
![]() 综上所述,“
综上所述,“![]() 牵手点”为
牵手点”为![]() 或
或![]()


科目:初中数学 来源: 题型:
【题目】如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE=![]() c,这时我们把关于x的形如ax+
c,这时我们把关于x的形如ax+![]() cx+b=0的一元二次方程称为“勾系一元二次方程”.
cx+b=0的一元二次方程称为“勾系一元二次方程”.
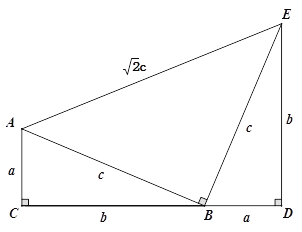
请解决下列问题:
写出一个“勾系一元二次方程”;
求证:关于x的“勾系一元二次方程”ax+![]() cx+b=0必有实数根;
cx+b=0必有实数根;
若x=1是“勾系一元二次方程”ax+![]() cx+b=0的一个根,且四边形ACDE的周长是
cx+b=0的一个根,且四边形ACDE的周长是![]() ,求△ABC面积.
,求△ABC面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红红有5张写着以下数字的卡片,请你按要求抽出卡片,解决下列问题:
![]()
(1)从中取出2张卡片,使这2张卡片上的数字相乘的积最大,最大值是________.
(2)从中取出2张卡片,使这2张卡片上的数字相除的商最小,最小值是________.
(3)从中取出0以外的4张卡片,将这4个数字进行加、减、乘、除或乘方等混合运算,使结果为24,(注:每个数字只能对用一次,如![]() )请另写出两种符合要求的运算式子.
)请另写出两种符合要求的运算式子.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在同一水平面从左到右依次是大厦、别墅、小山、小彬为了测得小山的高度,在大厦的楼顶B处测得山顶C的俯角∠GBC=13°,在别墅的大门A点处测得大厦的楼顶B点的仰角∠BAO=35°,山坡AC的坡度i=1:2,OA=500米,则山C的垂直高度约为( )(参考数据:sin13°≈0.22,tan13°≈0.23,sin35°≈0.57)
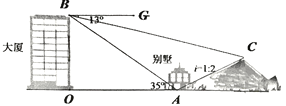
A. 161.0 B. 116.4 C. 106.8 D. 76.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两条直线AB,CD相交于点O,且![]() ,射线OM从OB开始绕O点逆时针方向旋转,速度为
,射线OM从OB开始绕O点逆时针方向旋转,速度为![]() ,射线ON同时从OD开始绕O点顺时针方向旋转,速度为
,射线ON同时从OD开始绕O点顺时针方向旋转,速度为![]() .两条射线OM、ON同时运动,运动时间为t秒.(本题出现的角均小于平角)
.两条射线OM、ON同时运动,运动时间为t秒.(本题出现的角均小于平角)
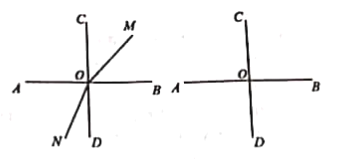
(1)当![]() 时,若
时,若![]() .试求出的值;
.试求出的值;
(2)当![]() 时,探究
时,探究![]() 的值,问:t满足怎样的条件是定值;满足怎样的条件不是定值?
的值,问:t满足怎样的条件是定值;满足怎样的条件不是定值?
查看答案和解析>>
科目:初中数学 来源: 题型:
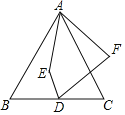
【题目】如图,等边△ABC中,AB=10,D为BC的中点,E为△ABC内一动点,DE=3,连接AE,将线段AE绕点A逆时针旋转60°得AF,连接DF,求线段DF的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂有新、旧两台机器,上半年,新机器平均每天比旧机器多生产50件产品,新机器生产600件产品所用的时间与旧机器生产450件产品所用的时间相同.
(1)求上半年新、旧机器日均产品数;
(2)下半年,新机器提高了生产效率,而旧机器由于不断损耗,生产效率降低,经测算,新机器日均产品数提高的百分数是旧机器日均产品数降低的百分数的2倍,结果新机器生产960件产品所用的时间与旧机器生产540件产品所用的时间相同,求新机器日均产品比旧机器多多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从5月份开始,水蜜桃和夏橙两种水果开始上市,根据市场调查,水蜜桃售价为20元/千克,夏橙售价为15元/千克.
(1)某水果商城抓住商机,开始销售这两种水果.若第一周水蜜桃的平均销量比夏橙的平均销量多100千克,要使该水果商城第一周销售这两周水果的总销售额不低于9000元,则第一周至少销售水蜜桃多少千克?
(2)若该水果商城第一周按照(1)中水蜜桃和夏橙的最低销量销售这两种水果,并决定第二周继续销售这两种水果.第二周水蜜桃售价降低了![]() ,销量比第一周增加了
,销量比第一周增加了![]() ,夏橙的售价保持不变,销量比第一周增加了
,夏橙的售价保持不变,销量比第一周增加了![]() .结果两种水果第二周的总销售额比第一周增加了
.结果两种水果第二周的总销售额比第一周增加了![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=-![]() x+6的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.
x+6的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.

(1)求点B的坐标;
(2)求直线AE的表达式;
(3)过点B作BF⊥AE,垂足为F,连接OF,试判断△OFB的形状,并求△OFB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com