
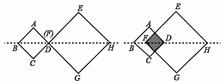
如图,四边形ABCD是边长为1 的正方形,四边形EFGH是边长为2的正方形,点D与点F重合,点B,D(F),H在同一条直线上,将正方形ABCD沿F→H方向平移至点B与点H重合时停止,设点D、F之间的距离为x,正方形ABCD与正方形EFGH重叠部分的面积为y,则能大致反映y与 x之间函数关系的图象是( )
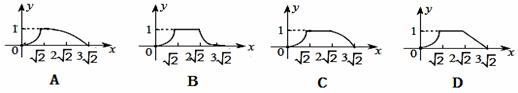
科目:初中数学 来源: 题型:
某手机店经销的Iphone5手机二月售价比一月每台降价500元.如果卖出相同数量的Iphone5手机,那么一月销售额为9万元,二月销售额只有8万元.
(1)一月Iphone5手机每台售价为多少元?
(2)为了扩大经营,该店计划三月购进Iphone5s手机销售,已知Iphone5每台进价为3500元,Iphone5s每台进价为4000元,该手机店打算用10万元再购进一批Iphone5和Iphone5s,问购进Iphone5手机10台后至多还能购进多少台Iphone5s?
查看答案和解析>>
科目:初中数学 来源: 题型:
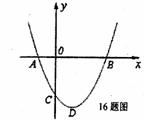
如图,二次函数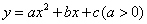 图象的顶点为
图象的顶点为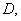 其图象与
其图象与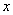 轴的交点为
轴的交点为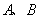 ,对称轴为直线x=1,与
,对称轴为直线x=1,与 轴负半轴交于点
轴负半轴交于点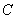 ,且OB=OC>2, 下面五个结论:
,且OB=OC>2, 下面五个结论:
①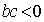 , ②
, ②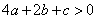 , ③
, ③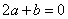 , ④
, ④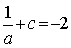 ,
,
⑤一元二次方程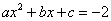 必有两个不相等的实数根.其中正确的结论是_ .
必有两个不相等的实数根.其中正确的结论是_ .
(只填序号,多填一个不得分,每少填一个扣2分)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1至图4中,两平行线AB、CD间的距离均为6,点M为AB上一定点.
思考:如图1,圆心为0的半圆形纸片在AB,CD之间(包括AB,CD),其直径MN在AB上,MN=8,点P为半圆上一点,设∠MOP=α。
当α=__ __度时,点P到CD的距离最小,最小值为__  __.
__.
探究一:在图1的基础上,以点M为旋转中心,在AB,CD 之间顺时针旋转该半圆形纸片,直到不能再转动为止,如图2,得到最大旋转角∠BMO=_ __度,此时点N到C D的距离是__ __.
D的距离是__ __.
探究二:将如图1中的扇形纸片NOP按下面对α的要求剪掉,使扇形纸片MOP绕点M在AB,CD之间顺时针旋转。
(1)如图3,当α=60°时,求 在旋转过程中,点P到CD的最小距离,并请指出旋转角∠BMO的最大值;
在旋转过程中,点P到CD的最小距离,并请指出旋转角∠BMO的最大值;
(2)如图4,在扇形纸片MOP旋转过程中,要保证点P能落在直线CD上,请直接确定α的最大值=__ __.

查看答案和解析>>
科目:初中数学 来源: 题型:
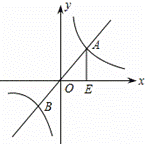
如图,已知函数y=2x和函数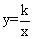 的图象交于A、B两点,过点A作AE⊥x轴于点E,若△AOE的面积为4,P是坐标平面上的点,且以点B、O、E、P为顶点的四边形是平行四边形,则满足条件的P点坐标是 .
的图象交于A、B两点,过点A作AE⊥x轴于点E,若△AOE的面积为4,P是坐标平面上的点,且以点B、O、E、P为顶点的四边形是平行四边形,则满足条件的P点坐标是 .
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com