Question

13．已知圆C的周长被y轴平分，且经过点A（$\sqrt{3}$，0），B（0，3）
（1）求圆C的方程；
（2）过原点O作直线l₁：y=k₁x交圆C于点E（x₁，y₁），F（x₂，y₂），作直线l₂：y=k₂x交圆C于点G（x₃，y₃），H（x₄，y₄），（其中y₂＞0，y₄＞0），设EH交x轴于点Q，GF交x轴于点R（如图）
①求证：$\frac{{k}_{1}{x}_{1}{x}_{2}}{{x}_{1}+{x}_{2}}$=$\frac{{k}_{2}{x}_{3}{x}_{4}}{{x}_{3}+{x}_{4}}$
②求证：|OQ|=|OR|（证明过程不考虑EH或GF垂直于x轴的情形）

Answer 1

分析 （1）设点P是⊙C上一点坐标为（x，y），连接AC，利用勾股定理求出⊙C半径，根据PC=2，列出等式即可．
（2）将直线EF和GH的方程分别代入圆C方程，利用韦达定理分别求得交点横坐标之和与之积，进而代入，证明原式．
（3）设点Q（q，0），点Q（r，0），由E、Q、H三点共线求得q的表达式，根据F、R、G三点共线求得r的表达式，进而根据（2）中的
整理得，进而可知q+r=0，所以|q|=|r|，即|OQ|=|OR|．

解答 解：（Ⅰ）设点P是⊙C上一点坐标为（x，y），连接AC，设⊙C半径为r，
在Rt△AOC中，∵AC²=OC²+OA²，
∴r²=（3-r）²+（$\sqrt{3}$）²，
∴r=2，
∴点C坐标（0，1），PC=2，
∴x²+（y-1）²=，4，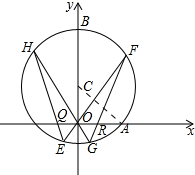
整理得x²+y²-2y-3=0
∴⊙C的方程为x²+y²-2y-3=0．

（Ⅱ）将直线EF的方程y=k₁x代入圆C方程
整理得（k₁²+1）x²-2k₁x-3=0
根据根与系数的关系得，（k₁²+1）x²-2k₁x-3=0
∴x₁+x₂=$\frac{2{k}_{1}}{{{k}^{2}}_{1}+1}$，x₁x₂=-$\frac{3}{{{k}_{1}}^{2}+1}$①
将直线GH的方程y=k₂x代入圆C方程，
同理可得，（k₂²+1）x²-2k₂x-3=0
∴x₃+x₄=$\frac{2{k}_{2}}{{{k}_{2}}^{2}+1}$，x₃x₄=-$\frac{3}{{{k}_{2}}^{2}+1}$②
由①、②可得，$\frac{{k}_{1}{x}_{1}{x}_{2}}{{x}_{1}+{x}_{2}}$=-$\frac{3}{2}$，$\frac{{k}_{2}{x}_{3}{x}_{4}}{{x}_{3}+{x}_{4}}$=-$\frac{3}{2}$，
∴$\frac{{k}_{1}{x}_{1}{x}_{2}}{{x}_{1}+{x}_{2}}$=$\frac{{k}_{2}{x}_{3}{x}_{4}}{{x}_{3}+{x}_{4}}$．

（Ⅲ）设点Q（q，0），点Q（r，0），由E、Q、H三点共线
得$\frac{{x}_{1}-q}{{k}_{1}{x}_{1}}$=$\frac{{x}_{4}-q}{{k}_{2}{x}_{4}}$，解得q=$\frac{（{k}_{1}-{k}_{2}）{x}_{1}{x}_{4}}{{k}_{1}{x}_{1}-{k}_{2}{x}_{4}}$
由F、R、G三点共线
同理可得 r=$\frac{（{k}_{1}-{k}_{2}）{x}_{2}{x}_{3}}{{k}_{1}{x}_{2}-{k}_{2}{x}_{3}}$
由 $\frac{{k}_{1}{x}_{1}{x}_{2}}{{x}_{1}+{x}_{2}}$=$\frac{{k}_{2}{x}_{3}{x}_{4}}{{x}_{3}+{x}_{4}}$变形得 $\frac{{x}_{2}{x}_{3}}{{k}_{1}{x}_{2}-{k}_{2}{x}_{3}}$=$\frac{-{x}_{1}{x}_{4}}{{k}_{1}{x}_{1}-{k}_{2}{x}_{4}}$
即$\frac{（{k}_{1}-{k}_{2}）{x}_{2}{x}_{3}}{{k}_{1}{x}_{2}-{k}_{2}{x}_{3}}$+$\frac{（{k}_{1}-{k}_{2}）{x}_{1}{x}_{4}}{{k}_{1}{x}_{2}-{k}_{2}{x}_{4}}$，
从而q+r=0，
所以|q|=|r|，
即|OQ|=|OR|．

点评 本题主要考查了圆的综合应用．涉及直线与圆的关系常需要把直线方程与圆方程联立，利用韦达定理来解决问题，对于初中生来说有一定难度．