练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    . 阅读材料：

    小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如3+2=（1+），善于思考的小明进行了以下探索：

    设a+b=（m+n）（其中a、b、m、n均为正整数）,则有a+b=m2+2n2+2mn,

    ∴a= m2+2n2,b=2mn.这样小明就找到了一种把部分a+b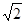的式子化为平方式的方法.

    请你仿照小明的方法探索并解决下列问题：

    （1）当a、b、m、n均为正整数时，若a+b=（m+n）,用含m、n的式子分别表示a、b，得：a=          ，      b=              ；

    （2）利用所探索的结论，找一组正整数a、b、m、n填空：        +       

    =（    ＋        ）；

    （3）若a+4=（m+n），且a、m、n均为正整数，求a的值.

     

     

     

    解：（1）a= m2+3n2           b=2mn  

    （2）4,2,1,1（答案不唯一）

    （3）根据题意得，∵2mn=4，且m、n为正整数，

    ∴m=2，n=1或m=1，n=2.∴a=13或7.

    解析:

    此题有一定的综合性。需要学生根据题意找出规律。

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：阅读理解

    阅读材料：
    小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如3+2
    		2
    =（1+
    		2
    ）2．善于思考的小明进行了以下探索：
    设a+b
    		2
    =（m+n
    		2
    ）2（其中a、b、m、n均为整数），则有a+b
    		2
    =m2+2n2+2mn
    		2
    ．
    ∴a=m2+2n2，b=2mn．这样小明就找到了一种把类似a+b
    		2
    的式子化为平方式的方法．
    请你仿照小明的方法探索并解决下列问题：
    （1）当a、b、m、n均为正整数时，若a+b
    		3
    =(m+n
    		3
    )    2    ，用含m、n的式子分别表示a、b，得：a=
     
    ，b=
     
    ；
    （2）利用所探索的结论，找一组正整数a、b、m、n填空：
     
    +
     
    		3
    =（
     
    +
     
    		3
    ）2；
    （3）若a+4
    		3
    =(m+n
    		3
    )    2    ，且a、m、n均为正整数，求a的值？

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    （2011•绍兴县模拟）阅读材料：
    小明在做课本阅读材料中的一个拼图游戏“对于任意剪一个三角形纸片，把这个三角形纸片剪2刀，分成3块，再把它们拼成一个长方形．”时遇到了困难，经提示他想到从特殊到一般的数学思想，于是他先剪了一个直角三角形纸片，把这个直角三角形纸片沿中位线剪1刀，分成2块（如图1），很快就拼成了一个与原三角形面积相等的矩形．
    解决问题：（请在图中画出分割线及拼成的图形）

    （1）请你在图2中用类似的方法把三角形剪一刀分成2块，然后拼成平行四边形；
    （2）请你在图3中把三角形剪两刀分成3块，然后拼成矩形；
    （3）应用拓展：
    如图4是一个正方形纸片，把这个正方形纸片剪2刀，分成3块，再拼成一个与原正方形面积相等的三角形，且该三角形既不是等腰三角形，也不是直角三角形（给出两种不同的方案）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    阅读材料： 小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如：3＋2＝(1＋)2，善于思考的小明进行了以下探索：

    设a＋b＝(m＋n)2(其中a、b、m、n均为整数)，则有a＋b＝m2＋2n2＋2mn.

    ∴a＝m2＋2n2，b＝2mn.这样小明就找到了一种把部分a＋b的式子化为平方式的方法．

    请你仿照小明的方法探索并解决下列问题：

    (1)当a、b、m、n均为正整数时，若a＋b＝(m＋n)2，用含m、n的式子分别表示a、b，得a＝________，b＝________；

    (2)利用所探索的结论，找一组正整数a、b、m、n，填空：________＋________＝(______＋______)2；

    (3)若a＋4＝(m＋n)2，且a、m、n均为正整数，求a的值．

    查看答案和解析>>

    科目：初中数学 来源：2012届广东省汕头市峡山街道模拟考试数学试卷（带解析） 题型：解答题

    阅读材料：
    小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如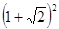： ，善于思考的小明进行了以下探索：
    设 （其中均为整数），则有
    ． ∴，．
    这样小明就找到了一种把部分的式子化为平方式的方法．
    请你仿照小明的方法探索并解决下列问题：
    （1）当均为正整数时，若，用含的式子分别表示，得＝_      ，＝_      ；
    （2）利用上面结论，找一组正整数，填空_  ＋_  ＝(_  ＋_  )；
    （3）若 ，且均为正整数，求a的值．

    查看答案和解析>>

    科目：初中数学 来源：2013年初中毕业升学考试（贵州黔西南卷）数学（解析版） 题型：解答题

    阅读材料： 小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如：，善于思考的小明进行了以下探索：

     设（其中均为整数），则有 ．

    ∴．这样小明就找到了一种把部分的式子化为平方式的方法．

    请你仿照小明的方法探索并解决下列问题：

    当均为正整数时，若，用含m、n的式子分别表示，得 ＝　    　，＝　    　；

    （2）利用所探索的结论，找一组正整数，填空：    ＋　  　＝(　  　＋　  　)2；

    （3）若，且均为正整数，求的值．

     

    查看答案和解析>>

    同步练习册答案