
��ͼ����ƽ��ֱ������ϵ�У�������y=��x2��2x+3���ύ��A��B���㣬��y�ύ�ڵ�C����DΪ�����ߵĶ��㣮
��1����ֱ��AC�Ľ���ʽ����ֱ��д��D������꣮
��2����ͼ1����ֱ��AC���Ϸ�����������һ����P����P����PQ��ֱ��x�ύAC�ڵ�Q��PM��BD��AC�ڵ�M��
�����PQM�ܳ����ֵ��
�ڵ���PQM�ܳ�ȡ�����ֵʱ��PQ��x�ύ��ΪH����λ˳������P��H��O��D�����ı��Σ������ܳ�ΪL�����߶�OH��x�����ƶ�����L��СֵʱOH�ƶ��ľ��뼰L����Сֵ��
��3����ͼ2������BD��y���ڵ�F������BOF�Ƶ�O��ʱ����ת������ת���������Ϊ��BOF�䣬B��F������ֱ����ֱ��AC��ֱ��OC�ֱ��ڵ�G��K������CGKΪֱ��������ʱ��ֱ��д���߶�BG�ij���


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2016�����ʡ�人���п�ģ����ѧ�Ծ��������������棩 ���ͣ������
���ֲ������ھ���ֽƬABCD�У�AB=3��AD=5����ͼ��ʾ���۵�ֽƬ��ʹ��A����BC���ϵ�A�䴦���ۺ�ΪPQ������A����BC�����ƶ�ʱ���ۺ۵Ķ˵�P��QҲ��֮�ƶ���������P��Q�ֱ���AB��AD�����ƶ������A����BC���Ͽ��ƶ���������Ϊ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�챱��ʮ���о��꼶��������ѧ�Ծ��������棩 ���ͣ�������
��ƽ��ֱ������ϵxOy�У������P��x��y���ı任��ΪP�䣨x+y��x��y����
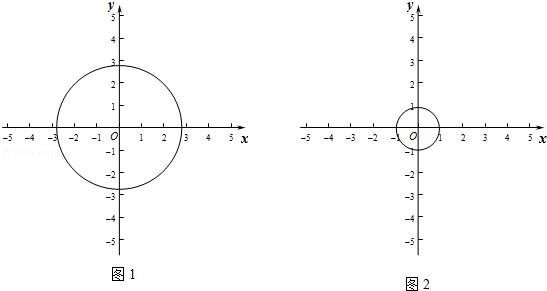
��1����ͼ1�������O�İ뾶Ϊ ��
��
�������ж�M��2��0����N����2����1��������ı任�����O��λ�ù�ϵ��
������P��ֱ��y=x+2�ϣ���P�ı任��P���ڡ�O���ڣ����P�������ȡֵ��Χ��
��2����ͼ2�������O�İ뾶Ϊ1����P�ı任��P����ֱ��y=��2x+6�ϣ����P���O������һ��������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�챱��ʮ���о��꼶��������ѧ�Ծ��������棩 ���ͣ������
�Ѷ��κ����ı���ʽy=x2��6x+5��Ϊy=a��x��h��2+k����ʽ����ôh+k= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�챱��ʮ���о��꼶��������ѧ�Ծ��������棩 ���ͣ�ѡ����
��ƽ��ֱ������ϵxOy�У������O����ԭ��O��0��0��ΪԲ�ģ���5Ϊ�뾶��Բ����ô��A����3����4�����O��λ�ù�ϵ�ǣ� ��
A���ڡ�O�� B���ڡ�O�� C���ڡ�O�� D������ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016���������ųɹ�ѧУ�п�һ����ѧ�Ծ��������棩 ���ͣ������
����
��1����x+2��2+��x+2����x��2����2��2x+1����3��x��
��2�� ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016���������ųɹ�ѧУ�п�һ����ѧ�Ծ��������棩 ���ͣ������
���㣨��1��2005��| ��2|+����
��2|+���� ����1��2sin60���ֵΪ ��
����1��2sin60���ֵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016�콭����ͨ���ʵ����ѧ�п���ģ��ѧ�Ծ��������棩 ���ͣ��ж���
���������κ���ͼ��Ķ��㣬���ڷ�����ͬ��������������κ���Ϊ��ͬ�ض��κ���������1����д������Ϊ��ͬ�ض��κ������ĺ�����
��2����֪����x�Ķ��κ���y1=2x2��4mx+2m2+1��y2=x2+bx+c������y1��ͼ����A��1��1������y1+y2��y1Ϊ��ͬ�ض��κ�����������y2�ı���ʽ������0��x��3ʱ��y2��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ������Ͽ������꼶������ģ����ѧ�Ծ��������棩 ���ͣ�ѡ����
��ͼ����ABO�У�AB��OB��OB= ��AB=1���ѡ�ABO�Ƶ�O��ת150���õ���A1B1O�����A1������Ϊ�� ��
��AB=1���ѡ�ABO�Ƶ�O��ת150���õ���A1B1O�����A1������Ϊ�� ��

A������1��-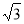 ��
��
B������1��-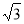 ����2��0��
����2��0��
C����-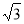 ����1����0����2��
����1����0����2��
D����-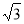 ����1��
����1��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com