
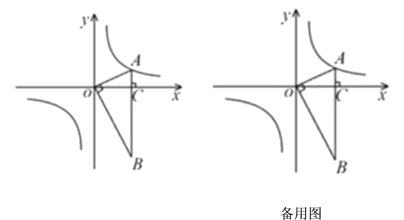
【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A(![]() ,1)在反比例函数y=
,1)在反比例函数y=![]() 的图像上.
的图像上.
(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)在x轴上是否存在一点P,使得SΔAOP=![]() SΔAOB,若存在求点P的坐标;若不存在请说明理由.
SΔAOB,若存在求点P的坐标;若不存在请说明理由.
(3)若将ΔBOA绕点B按逆时针方向旋转60°得到ΔBDE,直接写出点E的坐标,并判断点E是否在该反比例函数的图象上,说明理由.
【答案】(1)y=![]() ;(2)P(-2
;(2)P(-2![]() ,0)或(2
,0)或(2![]() ,0);(3)E(-
,0);(3)E(-![]() ,-1),点E在反比例函数y=
,-1),点E在反比例函数y=![]() 的图像上.
的图像上.
【解析】
(1)将点A(![]() ,1)代入y=
,1)代入y=![]() ,利用待定系数法即可求出反比例函数的表达式;
,利用待定系数法即可求出反比例函数的表达式;
(2)先由射影定理求出BC=3,那么AB=4,计算求出S△AOB,进而求出S△AOP.设点P的坐标为(m,0),列出方程求解即可;
(3)先解△OAB,得出∠ABO=30°,再根据旋转的性质求出E点坐标为(-![]() ,-1),即可求解.
,-1),即可求解.
(1)∵点A(![]() ,1)在反比例函数y=
,1)在反比例函数y=![]() 的图像上,
的图像上,
∴k=![]() ×1=
×1=![]() ,
,
∴y=![]() ;
;
(2)∵A(![]() ,1),
,1),
∴OC=![]() ,AC=1,
,AC=1,
由△OAC∽△BOC得OC2=ACBC可得BC=3,
∴BA=4,
∴SΔAOB=![]() ×
×![]() ×4=2
×4=2![]() ,
,
∵SΔAOP=![]() SΔAOB
SΔAOB
∴SΔAOP=![]() ,
,
设P(m,0)
∴![]() ×
×![]() ×1=
×1=![]() ,
,
∴![]() =2
=2![]() ,
,
∴m=-2![]() 或2
或2![]() ,
,
∴P(-2![]() ,0)或(2
,0)或(2![]() ,0) ;
,0) ;
(3)E(-![]() ,-1),点E在反比例函数y=
,-1),点E在反比例函数y=![]() 的图像上,
的图像上,
点E在该反比例函数的图象上,理由如下:
∵OA⊥OB,OA=2,OB=2![]() ,AB=4,
,AB=4,
∴sin∠ABO=![]() ,
,
∴∠ABO=30°,
∵将△BOA绕点B按逆时针方向旋转60°得到△BDE,
∴△BOA≌△BDE,∠OBD=60°,
∴BO=BD=2![]() ,OA=DE=2,∠BOA=∠BDE=90°,∠ABD=30°+60°=90°,
,OA=DE=2,∠BOA=∠BDE=90°,∠ABD=30°+60°=90°,
而BD-OC=![]() ,BC-DE=1,
,BC-DE=1,
∴E(-![]() ,-1),
,-1),
∵-![]() ×(-1)=
×(-1)=![]() ,
,
∴点E在该反比例函数的图象上.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
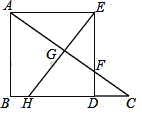
【题目】如图,在Rt△ABC中,∠B=90°,BC>AB,在BC边上取点D,使AB=BD,构造正方形ABDE,DE交AC于点F,作EG⊥AC交AC于点G,交BC于点H.
(1)求证:△AEF≌△EDH.
(2)若AB=3,DH=2DF,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,B在x轴上,四边形OACB为平行四边形,且
∠AOB=60°,反比例函数![]() (k>0)在第一象限内过点A,且与BC交于点F。当F为BC的中点,且S△AOF=12
(k>0)在第一象限内过点A,且与BC交于点F。当F为BC的中点,且S△AOF=12![]() 时,OA的长为____.
时,OA的长为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣5,1),B(﹣2,2),C(﹣1,4),请按下列要求画图:
(1)将△ABC先向右平移4个单位长度、再向下平移1个单位长度,得到△A1B1C1,画出△A1B1C1;
(2)画出与△ABC关于原点O成中心对称的△A2B2C2,并直接写出点A2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
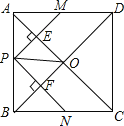
【题目】如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:
①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF;⑤当△PMN∽△AMP时,点P是AB的中点.
其中正确的结论有
A.5个 B.4个 C.3个 D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
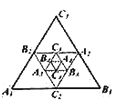
【题目】如图,小红作出了边长为1的第1个等边![]() ,算出了等边
,算出了等边![]() 的面积,然后分别取
的面积,然后分别取![]() 三边的中点
三边的中点![]() 、
、![]() 、
、![]() ,作出了第2个等边
,作出了第2个等边![]() ,算出了等边
,算出了等边![]() 的面积,用同样的方法,作出了第3个等边
的面积,用同样的方法,作出了第3个等边![]() ,算出了等边
,算出了等边![]() 的面积……,由此可得,第
的面积……,由此可得,第![]() 个等边
个等边![]() 的面积是( )
的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
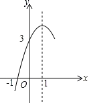
【题目】如图,抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,与
,与![]() 轴一个交点的坐标为(-1,0),其部分图象如图所示,下列结论:
轴一个交点的坐标为(-1,0),其部分图象如图所示,下列结论:
![]() ;
;![]() ;
;![]() 方程
方程![]() 的两个根是
的两个根是![]() ,
,![]() ;④当
;④当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() .其中结论正确的是_____________(填写正确结论的标号)
.其中结论正确的是_____________(填写正确结论的标号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】书法是我国的文化瑰宝,研习书法能培养高雅的品格.某校为加强书法教学,了解学生现有的书写能力,随机抽取了部分学生进行测试,测试结果分为优秀、良好、及格、不及格四个等级,分别用A,B,C,D表示,并将测试结果绘制成如图两幅不完整的统计图.
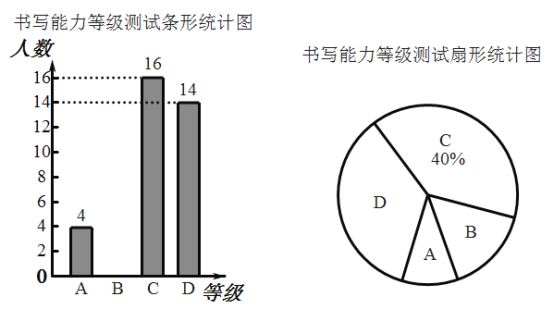
请根据统计图中的信息解答以下问题:
(1)本次抽取的学生人数是 人,扇形统计图中A所对应扇形圆心角的度数是 .
(2)把条形统计图补充完整.
(3)若该学校共有2800人,等级达到优秀的人数大约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
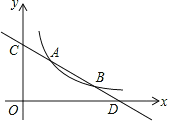
【题目】直线y=kx+b与反比例函数y=![]() (x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.
(x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.
(1)求直线AB的解析式;
(2)若点P是x轴上一动点,当△COD与△ADP相似时,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com