
分析 由不等式ax2+bx+c<0(a≠0)的解集为x<2或x>3,可得2,3为方程ax2+bx+c=0的两根,利用根与系数的关系得到系数的比,变形后得到b=-5a,c=6a.由此求出方程bx2+ax+c的两根,则不等式bx2+ax+c>0的解集可求.
解答 解:∵不等式ax2+bx+c<0(a≠0)的解是x<2,或x>3,
∴2,3为方程ax2+bx+c=0的两个实数根,且a<0.
∴$\left\{\begin{array}{l}{-\frac{b}{a}=2+3}\\{\frac{c}{a}=2×3}\end{array}\right.$,
则b=-5a,c=6a.
代入不等式bx2+ax+c>0可得-5ax2+ax+6a>0,
∵a<0.
∴-5x2+x+6<0,即-(x+1)(5x-6)<0,
解得x<-1或x>$\frac{6}{5}$,
即不等式bx2+ax+c>0的解集是x<-1或x>$\frac{6}{5}$.
点评 本题考查了一元二次不等式的解法、一元二次方程的根与系数的关系,考查了推理能力和计算能力,属于基础题.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:解答题
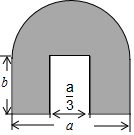 如图是一个工件的横断面及其尺寸.(单位:cm).
如图是一个工件的横断面及其尺寸.(单位:cm).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | {x|x≤-2或x≥$\frac{1}{2}$} | B. | {x|x≤-$\frac{1}{2}$或x≥2} | C. | {x|-$\frac{1}{2}$≤x≤2} | D. | {x|-2≤x≤$\frac{1}{2}$} |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com