
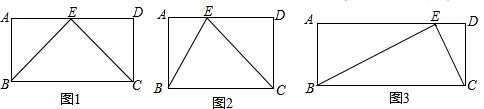
分析 (1)当点E运动到边AD的中点时,AE=AB,DE=DC,故此△AEB和△DEC为等腰直角三角形,从而可证明∠BEC=90°;
(2)以BC为直径作圆0,过点O作OF⊥AD垂足为F,可知r=1.5,OF=2,d>r,故此直线AD与圆0相离,所以∠BEC<90°;
(3)根据题意画出图形,然后根据相似三角形的性质列出比例式,从而可求得AE的长.
解答 解:(1)∵E是AD的中点,
∴AE=DE=2.
∵AB=DC=2.
∴AE=AB,DE=DC.
∵ABCD为矩形,
∴∠A=∠D=90°.
∴△AEB和△DEC均为等腰直角三角形.
∴∠AEB=45°,∠DEC=45°.
∴∠BEC=180°-45°-45°=90°.
∴BE⊥EC.
(2)不存在.
理由:以BC为直径作圆0,过点O作OF⊥AD垂足为F.
∵BC=3,
∴圆O的半径r=1.5,
∵∠ABO=∠A=∠OFA=90°,
∴四边形ABOF为矩形.
∴OF=AB=2.
∴d>r,
∴直线AD与圆0相离.
∴点E在圆O外.
∴∠BEC<90°;
(3)如图3所示.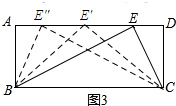
①设AE=x,则ED=5-x.
∵△EAB∽△CDE,
∴$\frac{DC}{ED}=\frac{AE}{AD}$,即$\frac{2}{5-x}=\frac{x}{2}$.
解得:x1=4,x2=1(舍去),
∴AE=4.
②当点E位于E′处时.
∵△AE′B∽△DE′C.
∴$\frac{AE′}{DE′}=\frac{AB}{DC}=1$.
∴AE′=DE′.
∴AE′=2.5,即AE=2.5.
③当点E位于E″处时.
∵△ABE″∽△DE″C,
∴$\frac{AE″}{AB}=\frac{DC}{DE″}$,即$\frac{x}{2}=\frac{2}{5-x}$.
解得:x1=1,x2=4(舍去).
综上所述,若以A,B,E为顶点的三角形与以D,C,E为顶点的三角形相似,AE=1或AE=2.5,或AE=4.
点评 本题主要考查的是矩形的性质、相似三角形的性质和判定、等腰直角三角形的性质和判定的综合应用,根据相似三角形的性质,结合点E的位置,列出关于AE长度的比例式是解题的关键.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:解答题
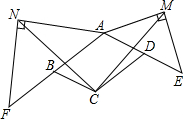 如图,已知在?ABCD中,延长AD到E,使DE=AD,延长AB到F,使BF=AB,分别以AF、AE为斜边作Rt△ANF,Rt△AME,且∠F=∠E.求证:CM=CN.
如图,已知在?ABCD中,延长AD到E,使DE=AD,延长AB到F,使BF=AB,分别以AF、AE为斜边作Rt△ANF,Rt△AME,且∠F=∠E.求证:CM=CN.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com