
����Ŀ����ͼ����ֱ������ABCD�У�AD // BC����B��90�㣬AD��24cm��BC��26cm������P��A�㿪ʼ��AD����D��3cm/s���ٶ��˶�������Q�ӵ�C��ʼ��CB�������1cm/s���ٶ��˶�����P��Q�ֱ��A��Cͬʱ���������˶�ʱ��Ϊt (s)��������һ�㵽��˵�ʱ����һ��Ҳ��ֹ֮ͣ�˶���

�ٵ�tΪ��ֵʱ����CD��PQΪ���ߣ������εĵף�AD��BC����һ���֣���ȫ����Ϊ�������ܹ���һ�������Σ�
�������tΪ��ֵʱ���ı���PQCDΪ�������Ρ�
���𰸡���1��t=0��t=8;(2) t=7
�����������������(1)CD��PQΪ�߹��������������Ա����������߶ζ˵����������Է�����������P,A;C,Q�غϣ�P,D�غ�.
(2) ����P��PF��BC�ڵ�F������D��DE��BC�ڵ�E,Ҫ���ɵ��������Σ�����![]() PQFȫ��
PQFȫ��![]() BCE.
BCE.
���������
�ٸ�������ã�
����P���A�غ�ʱ�ܹ���һ�������Σ���ʱt=0��
�ߵ�P����D���裺8(s)��
��Q����B���裺26(s)��
�൱��P���D�غ�ʱ�ܹ���һ�������Σ���ʱt=8s��
�ʵ�t=0��8sʱ,��CD��PQΪ����,�����εĵ�(AD��BC)��һ����(��ȫ��)Ϊ�������ܹ���һ��������.
�ڡ�BCAD=2cm��
����P��PF��BC�ڵ�F������D��DE��BC�ڵ�E��
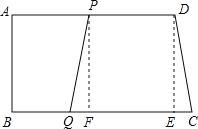
�ߵ�PQ=CDʱ���ı���PQCDΪ�������Σ�
����PFQ����DCE��EF=PD��
��QF=CE=2cm��
�൱CQPD=QF+CE=4cmʱ���ı���PQCDΪ�������Σ�
��t(243t)=4��
��t=7(s)��
�൱t=7sʱ���ı���PQCDΪ��������.


 Ӧ����㲦ϵ�д�
Ӧ����㲦ϵ�д� ״Ԫ����ϵ�д�
״Ԫ����ϵ�д� ͬ������ϵ�д�
ͬ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪:��ͼ,A��B��C��D Ϊ���ε��ĸ�����,AB��16cm��AD��
6cm������P��Q �ֱ��A��C ͬʱ����,��P ��3cm/s���ٶ����B �ƶ�,
һֱ����� B Ϊֹ,�� Q ��2cm/s���ٶ���� D �ƶ���
��1��P��Q ����ӳ������������ʱ,�ı���PBCQ �������33cm2?
��2��P��Q ����ӳ������������ʱ,��P��Q ��ľ�����10cm?

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����з����н�Ϊx=��2���ǣ� ��
A.3x��2=2x
B.4x��1=3
C.2x+1=x��1
D.x��4=0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����Ϊ8��������Ϊ5��������Ϊ7���ij�����������ȥһ����Ϊ6��������Ϊ5��������Ϊ2���ij���������õ�һ����ͼ��ʾ�ļ�������һֻ����Ҫ�Ӹü�����Ķ���A�������ż�����ı��浽�������Ϻ�A��ԵĶ���B����ʳ������ô����Ҫ���е����·���ij��� ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ε�һ�߳�Ϊ4cm����һ�߳�Ϊ10cm����˵��������ε��ܳ�Ϊ_________ cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˼�ǿ����Ľ�ˮ��ʶ����������ˮ��Դ��ij�ߵ�С����ֱ��ˮ���ü۸�����ֶ����ڴ��ﵽ��ˮ��Ŀ�ģ�����ͼ�Ǵ�С���Ծ���ֱ��ˮij����ˮ��x����ˮ��yԪ�ĺ���ͼ��ˮ�Ѱ��½��㣩��

��1�������

��2����ij������9�·���ˮ��Ϊ9.5�֣�����û�9�·�ˮ�ѣ�
��3����ij������11����ˮ![]() ���֣����ú�
���֣����ú�![]() �Ĵ���ʽ��ʾ�û�����11�¹�Ӧ��ˮ��Q��Ԫ��.
�Ĵ���ʽ��ʾ�û�����11�¹�Ӧ��ˮ��Q��Ԫ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУѧ�������г���ѧУȥij��ֲ��������һ��ʱ��ѧУ�ɺ�����Ա����ȥ�������ֲ�����ߣ�ѧ����������Ա�뿪ѧУ�ľ���y��ǧ�ף�����ʻʱ��x�����ӣ��ĺ���ͼ����ͼ��ʾ��

��1������ͼ����Ϣ����ѧ�������г����ٶȺͺ�����Ա�������ٶȣ�
��2��˵��B������岢���B������ꣻ
��3������ֱ��д��ѧ�������������Ա�����˶������3ǧ��ʱ�䣮
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com