
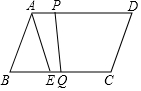
 如图,四边形ABCD为平行四边形,在BC上取一点E,连接AE,∠ABC=∠DAE.点P从点B出发,沿B-A-D-A运动,沿B-A运动时的速度为13cm/s,沿A-D-A运动时的速度为8cm/s.点Q从点B出发沿BC方向运动,运动速度为5cm/s,P,Q两点同时从点B出发,当点Q到达点C时,P,Q两点同时停止运动.设点P的运动时间为t(s),连接PQ,已知AB=26cm,BC=40cm,点A到边BC的距离为24cm.
如图,四边形ABCD为平行四边形,在BC上取一点E,连接AE,∠ABC=∠DAE.点P从点B出发,沿B-A-D-A运动,沿B-A运动时的速度为13cm/s,沿A-D-A运动时的速度为8cm/s.点Q从点B出发沿BC方向运动,运动速度为5cm/s,P,Q两点同时从点B出发,当点Q到达点C时,P,Q两点同时停止运动.设点P的运动时间为t(s),连接PQ,已知AB=26cm,BC=40cm,点A到边BC的距离为24cm.分析 (1)根据平行四边形性质得:AD∥BC,再由平行线性质得:∠DAE=∠AEB,从而得AB=AE;
(2)先计算点P在走完AB所用的时间:26÷13=2s,点P走完AD时所用的时间:40÷8=5s,分别写出点P在线段AD上时和线段DA上时对应的AP的长;
(3)根据AD∥BC可知:只要PD=CQ,则四边形PDCQ就能成为平行四边形,因此将点P在三条线段上运动时,分三种情况进行讨论:分别表示PD和CQ的长,列式计算可求出结果;
(4)分两种情况计算:当0<t<2时,如图2,S=$\frac{1}{2}$AP•QF;当2<t<7时,如图3,S=$\frac{1}{2}$AP×24;分别代入计算即可.
解答 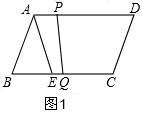 解:(1)∵四边形ABCD为平行四边形,
解:(1)∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB,
∵∠ABC=∠DAE,
∴∠ABC=∠AEB,
∴AB=AE;
(2)点P从B到A时,t=$\frac{26}{13}$=2s,
点P从A到D时,t=$\frac{40}{8}$=5s,
当点P从点A到D时,AP=8(t-2)=8t-16,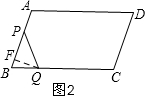
当点P从D到A时,AP=40-8(t-2-5)=-8t+96;
(3)∵AD∥BC,
∴当四边形PDCQ是平行四边形时,满足PD=CQ,
①当0<t<2时,点P在线段AB上,不存在四边形PDCQ为平行四边形,
②当2≤t≤7时,点P在线段AD上,且P从A→D运动,
此时AP=8t-16,BQ=5t,
∴PD=40-(8t-16),QC=40-5t,
∴40-(8t-16)=40-5t,
t0=$\frac{16}{3}$,
③当7<t≤12时,点P在线段AD上,且P从D→A运动,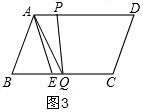
此时,AP=96-8t,PD=40-(96-8t),
∴40-(96-8t)=40-5t,
t0=$\frac{96}{13}$,
综上所述,当t0=$\frac{16}{3}$s或$\frac{96}{13}$s时,四边形PDCQ能成为平行四边形;
(4)当0<t<2时,如图2,
此时AP=26-13t,BQ=5t,
过Q作QF⊥AB于F,
S△ABC=$\frac{1}{2}$AB•QF=$\frac{1}{2}$BQ×24,
26QF=5t×24,
QF=$\frac{60}{13}$t,
∴S=$\frac{1}{2}$AP•QF=$\frac{1}{2}$(26-13t)$•\frac{60}{13}t$=-30t2+60t,
当2<t<7时,如图3,
S=$\frac{1}{2}$AP×24=$\frac{1}{2}$×(8t-16)×24=96t-192;
综上所述,S与t之间的函数关系式为:S=$\left\{\begin{array}{l}{-30{t}^{2}+60t(0<t<2)}\\{96t-192(2<t<7)}\end{array}\right.$.
点评 本题是四边形的综合题,难度适中,考查了平行四边形、动点问题和三角形的面积,注意动点线段的表示方法,同时也考查了学生对知识的综合运用能力.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
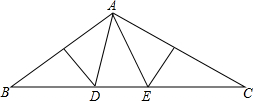 如图,△ABC的两边AB、AC的垂直平分线分别交边BC于点D、E,若△ABC的周长为26,AB+AC=14,则△ABE和△ACD的周长和是38.
如图,△ABC的两边AB、AC的垂直平分线分别交边BC于点D、E,若△ABC的周长为26,AB+AC=14,则△ABE和△ACD的周长和是38.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com