Question

如图1，已知梯形OABC，抛物线分别过点O（0，0）、A（2，0）、B（6，3）．

（1）直接写出抛物线的对称轴、解析式及顶点M的坐标；

（2）将图1中梯形OABC的上下底边所在的直线OA、CB以相同的速度同时向上平移，分别交抛物线于点O₁、A₁、C₁、B₁，得到如图2的梯形O₁A₁B₁C₁．设梯形O₁A₁B₁C₁的面积为S，A₁、 B₁的坐标分别为 (x₁，y₁)、(x₂，y₂)．用含S的代数式表示－，并求出当S=36时点A₁的坐标；

（3）在图1中，设点D坐标为(1，3)，动点P从点B出发，以每秒1个单位长度的速度沿着线段BC运动，动点Q从点D出发，以与点P相同的速度沿着线段DM运动．P、Q两点同时出发，当点Q到达点M时，P、Q两点同时停止运动．设P、Q两点的运动时间为t，是否存在某一时刻t，使得直线PQ、直线AB、轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似？若存在，请求出t的值；若不存在，请说明理由．

                                                    

                                                    

Answer 1

解：（1）对称轴：直线

解析式：或

                  顶点坐标：M（1，）

            （2）由题意得       

3

得：①

  

得：  ②

把②代入①并整理得：(S＞0) (事实上，更确切为S＞6)

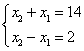当时， 解得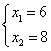：(注：S＞0或S＞6不写不扣

分)  把代入抛物线解析式得       ∴点A₁（6，3）

（3）存在

           解法一：易知直线AB的解析式为，可得直线AB与对称轴的

交点E的坐标为

∴BD=5，DE=，DP=5－t，DQ= t

     当∥时，

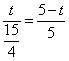                得

    下面分两种情况讨论: 设直线PQ与直线AB、x轴的交点分别为点F、G

①当时，如图1-1        ∵△FQE∽△FAG  ∴∠FGA＝∠FEQ

               ∴∠DPQ＝∠DEB   易得△DPQ∽△DEB  ∴

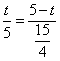∴   得   ∴(舍去)

②     当时，如图1-2

∵△FQE∽△FAG  ∴∠FAG＝∠FQE

                ∵∠DQP＝∠FQE    ∠FAG＝∠EBD

∴∠DQP＝∠DBE   易得△DPQ∽△DEB

       ∴

     ∴，    ∴

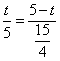                           ∴当秒时，使直线、直线、轴围成的三角形与直线、直线、抛物线的对称轴围成的三角形相似

                            (注:未求出能得到正确答案不扣分)

                             解法二：可将向左平移一个单位得到,再用解法一类似的方法可求得

                                     , ,

                                    ∴