

分析 (1)设生产A种品质的醋x缸,生产B种品质的醋(10-x)缸,先表示出生产这10缸醋的购买甲乙两种粮食的费用为1.5×[300x+200(10-x)]+2.5×[100x+200(10-x)],根据作坊计划用于甲、乙两种粮食资金不超过7500元,列出不等式组,然后解两个不等式求出其公共部分得到5≤x<8,而x为整数,则x的值为5,6,7,易得符合条件的生产方案;
(2)设总生产成本为W元,加工费为:200x+300(10-x),则W=1.5×[300x+200(10-x)]+2.5×[100x+200(10-x)]+200x+300(10-x)=-200X+11000,根据一次函数的性质得到W随x的增大而减小,然后把x=5代入,即可得到最低成本的生产方案.
解答 解:(1)设生产A种品质的醋x缸,生产B种品质的醋(10-x)缸,
生产这10缸醋的购买甲乙两种粮食的费用为:1.5×[300x+200(10-x)]+2.5×[100x+200(10-x)],
根据题意得:0<1.5×[300x+200(10-x)]+2.5×[100x+200(10-x)]≤7500,
解得:5≤x<8,
∴x=5、6、7,
共有三种方案:
①生产A种品质的醋5缸,生产B种品质的醋5缸;
②生产A种品质的醋6缸,生产B种品质的醋4缸;
③生产A种品质的醋7缸,生产B种品质的醋8缸;
(2)设生产A种品质的醋x缸,生产B种品质的醋(10-x)缸,总生产成本为W元,加工费为:200x+300(10-x),
则W=1.5×[300x+200(10-x)]+2.5×[100x+200(10-x)]+200x+300(10-x)=-200X+11000,
∵-200<0,
∴W随x的增大而减小,
而x=5,6,7,
∴当x=5时,总成本最低,最低成本为11000元.
答:使生产这10缸醋的成本最低,应选择生产A种品质的醋5缸,生产B种品质的醋5缸,最低成本为11000元.
点评 本题考查了一次函数的应用:通过实际问题列出一次函数关系式,然后根据一次函数的性质解决问题.也考查了二元一次方程组以及一元一次不等式组的应用.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案科目:初中数学 来源: 题型:解答题
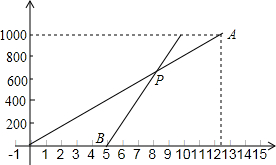 小明每天早上步行到学校上学,一天,小明从家里出发后5分钟,他爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度沿相同路线去追小明,设小明离开家的时间为x(分),如图所示的线段OA表示小明从家到学校的过程中离开家的距离y1(米)与x(分)的关系;线段BP表示爸爸追赶小明时离开家的距离y2(米)与x(分)之间的关系.请分析图中的信息解答下列问题:
小明每天早上步行到学校上学,一天,小明从家里出发后5分钟,他爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度沿相同路线去追小明,设小明离开家的时间为x(分),如图所示的线段OA表示小明从家到学校的过程中离开家的距离y1(米)与x(分)的关系;线段BP表示爸爸追赶小明时离开家的距离y2(米)与x(分)之间的关系.请分析图中的信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 业务种类 | 计费单位 | 资费标准/元 | |
| 本埠资费 | 外埠资费 | ||
| 信函 | 首重100克内,每重20克(不足20克按20克计算) | 0.80 | 1.20 |
| 续重101-2000克每重100克(不足100克按100克计算) | 1.20 | 2.00 | |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
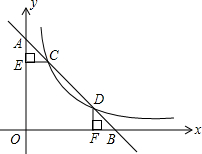 如图,一次函数的图象与x轴,y轴交于点B,A,与反比例函数y=$\frac{12}{x}$在第一象限内的图象交于点C(m,m+1),D(n,2),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F.
如图,一次函数的图象与x轴,y轴交于点B,A,与反比例函数y=$\frac{12}{x}$在第一象限内的图象交于点C(m,m+1),D(n,2),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com