
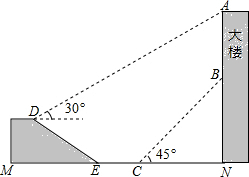
分析 (1)利用坡度和DE直接求出D点距水平面EN的高度;
(2)借助(1)得出的结论,可求出DH的长,在直角三角形ADH中,可求出AH的长,进而可求出AN的长,在直角三角形CNB中可求出BN的长,利用AB=AH-BN计算即可.
解答 解:(1)如图, 过点D作DG⊥MN于G,
过点D作DG⊥MN于G,
在Rt△DEG中,坡面DE=20米,山坡的坡度i=1:$\sqrt{3}$,
∴tan∠DEM=$\frac{DG}{EG}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠DEM=30°,
∴EG=10$\sqrt{3}$米,DG=$\frac{1}{2}$DE=10米;
∴D点距水平面EN的高度为10米.
(2)如图,过点D作DH⊥AN于H,
由(1)知,DG=10米,EG=10$\sqrt{3}$米,
∵DH=EG+EC+CN=(10$\sqrt{3}$+30)米,∠ADH=30°,
∴AH=$\frac{\sqrt{3}}{3}$×DH=(10+10$\sqrt{3}$)米,
∴AN=AH+DG=(20+10$\sqrt{3}$)米,
∵∠BCN=45°,
∴CN=BN=20米,
∴AB=AN-BN=10$\sqrt{3}$≈17米,
答:条幅AB的长度是17米.
点评 此题是解直角三角形的应用--仰角,俯角问题,主要考查了仰角、坡度的定义,能够正确地构建出直角三角形,将实际问题化归为解直角三角形的问题是解答此类题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
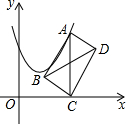 如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动,点C在x轴上运动,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为( )
如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动,点C在x轴上运动,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 日 期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数变化(万人) | +0.5 | +0.7 | +0.8 | -0.4 | -0.6 | +0.2 | -0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com