
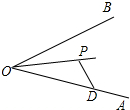
 如图,已知点P为∠AOB的角平分线上的一点,点D在边OA上.爱动脑筋的小刚经过仔细观察后,进行如下操作:在边OB上取一点E,使得PE=PD,这时他发现∠OEP与∠ODP之间有一定的相等关系,请你写出∠OEP与∠ODP所有可能的数量关系.
如图,已知点P为∠AOB的角平分线上的一点,点D在边OA上.爱动脑筋的小刚经过仔细观察后,进行如下操作:在边OB上取一点E,使得PE=PD,这时他发现∠OEP与∠ODP之间有一定的相等关系,请你写出∠OEP与∠ODP所有可能的数量关系. 分析 结论:∠OEP=∠ODP或∠OEP+∠ODP=180?以O为圆心,以OD为半径作弧,交OB于E2,连接PE2,由△E2OP≌△DOP(SAS),推出E2P=PD,即此时点E2符合条件,此时∠OE2P=∠ODP;以P为圆心,以PD为半径作弧,交OB于另一点E1,连接PE1,则此点E1也符合条件PD=PE1,由PE2=PE1=PD,
推出∠PE2E1=∠PE1E2,由∠OE1P+∠E2E1P=180°,∠OE2P=∠ODP,推出∠OE1P+∠ODP=180°,
解答 解:结论:∠OEP=∠ODP或∠OEP+∠ODP=180°.
理由是:以O为圆心,以OD为半径作弧,交OB于E2,连接PE2,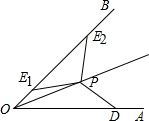
∵在△E2OP和△DOP中,
$\left\{\begin{array}{l}{O{E}_{2}=OD}\\{∠{E}_{2}OP=∠DOP}\\{OP=OP}\end{array}\right.$,
∴△E2OP≌△DOP(SAS),
∴E2P=PD,
即此时点E2符合条件,此时∠OE2P=∠ODP;
以P为圆心,以PD为半径作弧,交OB于另一点E1,连接PE1,
则此点E1也符合条件PD=PE1,
∵PE2=PE1=PD,
∴∠PE2E1=∠PE1E2,
∵∠OE1P+∠E2E1P=180°,
∵∠OE2P=∠ODP,
∴∠OE1P+∠ODP=180°,
∴∠OEP与∠ODP所有可能的数量关系是:∠OEP=∠ODP或∠OEP+∠ODP=180°,
点评 本题考查全等三角形的判定和性质,等腰三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第一次 | 第二次 | |
| 甲种车辆数单位(辆) | 2 | 5 |
| 乙种车辆数单位(辆) | 3 | 6 |
| 累计运货数单位(吨) | 15.5 | 35 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
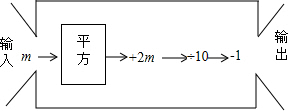
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在数学课上,老师提出如下问题:
在数学课上,老师提出如下问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com