
 将正整数按如图所示的规律排列下去,若有序实数对(4,3)表示实数9,则表示的实数是58的有序实数对为(11,3).
将正整数按如图所示的规律排列下去,若有序实数对(4,3)表示实数9,则表示的实数是58的有序实数对为(11,3).  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
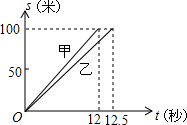 甲乙两人在一次100米赛跑中的路程s(米)和时间t(秒)的函数关系如图所示.
甲乙两人在一次100米赛跑中的路程s(米)和时间t(秒)的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
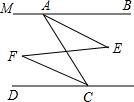 如图,已知AB∥CD,∠MAC=100°.
如图,已知AB∥CD,∠MAC=100°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1:2:1:2 | B. | 1:2:2:1 | C. | 1:2:3:4 | D. | 1:1:2:2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,如果顾客乘地铁从点B到点C上升的高度为5m,则电梯BC的长是( )
如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,如果顾客乘地铁从点B到点C上升的高度为5m,则电梯BC的长是( )| A. | 5cm | B. | 5$\sqrt{3}$cm | C. | 10m | D. | $\frac{10\sqrt{3}}{3}$m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
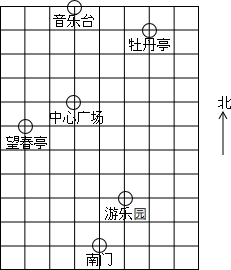 春天到了,七(1)班组织同学到人民公园春游,张明、李华对着景区示意图描述牡丹亭位置(图中小正方形边长代表100m)
春天到了,七(1)班组织同学到人民公园春游,张明、李华对着景区示意图描述牡丹亭位置(图中小正方形边长代表100m)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com