
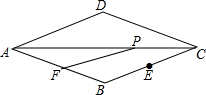
 如图,菱形ABCD中,∠D=135°,AD=6,CE=2$\sqrt{2}$,点P是线段AC上一动点,点F是线段AB上一动点,则PE+PF的最小值是( )
如图,菱形ABCD中,∠D=135°,AD=6,CE=2$\sqrt{2}$,点P是线段AC上一动点,点F是线段AB上一动点,则PE+PF的最小值是( )| A. | 3 | B. | 6 | C. | 2$\sqrt{5}$ | D. | 3$\sqrt{2}$ |
分析 先作点E关于AC的对称点点G,再连接BG,过点B作BH⊥CD于H,运用勾股定理求得BH和GH的长,最后在Rt△BHG中,运用勾股定理求得BG的长,即为PE+PF的最小值.
解答 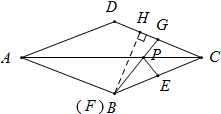 解:作点E关于AC的对称点点G,连接PG、PE,则PE=PG,CE=CG=2$\sqrt{2}$,
解:作点E关于AC的对称点点G,连接PG、PE,则PE=PG,CE=CG=2$\sqrt{2}$,
连接BG,过点B作BH⊥CD于H,则∠BCH=∠CBH=45°,
∴Rt△BHC中,BH=CH=$\frac{6}{\sqrt{2}}$=3$\sqrt{2}$,
∴HG=3$\sqrt{2}$-2$\sqrt{2}$=$\sqrt{2}$,
∴Rt△BHG中,BG=$\sqrt{(3\sqrt{2})^{2}+(\sqrt{2})^{2}}$=$\sqrt{20}$=2$\sqrt{5}$,
∵当点F与点B重合时,PE+PF=PG+PB=BG(最短),
∴PE+PF的最小值是2$\sqrt{5}$.
故选(C)
点评 本题以最短距离问题为背景,主要考查了菱形的性质与轴对称的性质,凡是涉及最短距离的问题,一般要考虑线段的性质定理,一般情况要作点关于某直线的对称点.注意:如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:选择题
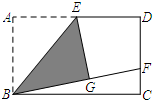 如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=2,FD=4,则BC的长为( )
如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=2,FD=4,则BC的长为( )| A. | 6$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{5}$ | D. | 4$\sqrt{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com