
分析 (1)将y=0代入y=-$\frac{1}{2}$x+1,求出x的值,得到点A的坐标,将x=0代入y=-$\frac{1}{2}$x+1,求出y的值,得到点B的坐标;
(2)根据一次函数的性质,过A,B两点画直线即可;
(3)结合(2)中的图沿y轴向下平移3个单位画出直线即可;
(4)先根据直线平移的规律,将y=-$\frac{1}{2}$x+1向下平移三个单位后得到y=-$\frac{1}{2}$x-2.
解答 解:(1)将y=0代入y=-$\frac{1}{2}$x+1,
得-$\frac{1}{2}$x+1=0,
解得x=2,
则点A的坐标为(2,0).
将x=0代入y=-$\frac{1}{2}$x+1,
得y=-$\frac{1}{2}$×0+1=1,
则点B的坐标为(0,1).
故答案为A(2,0),B(0,1);
(2)如下图: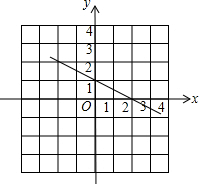
(3)将y=-$\frac{1}{2}$x+1向下平移3个单位后得到的图象如图.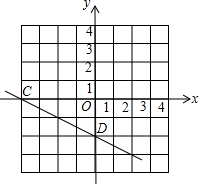
(4)将y=-$\frac{1}{2}$x+1向下平移三个单位后得到y=-$\frac{1}{2}$x-2.
点评 本题考查了一次函数图象上点的坐标特征,一次函数的图象与性质,一次函数图象与几何变换,都是基础知识,需熟练掌握.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 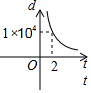 | B. | 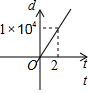 | C. | 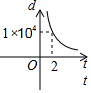 | D. | 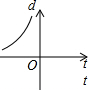 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
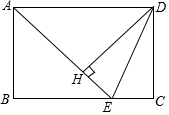 如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接DE,下列结论:①∠AED=∠CED;②△AED为等腰三角形;③EH=CE;④图中有3个等腰三角形.结论正确的个数为( )
如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接DE,下列结论:①∠AED=∠CED;②△AED为等腰三角形;③EH=CE;④图中有3个等腰三角形.结论正确的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
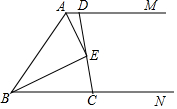 如图,AM∥BN,∠MAB和∠NBA的平分线交于E点.求:
如图,AM∥BN,∠MAB和∠NBA的平分线交于E点.求:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
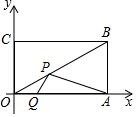 已知在平面直角坐标系中,矩形OABC的顶点O为坐标原点,顶点A、B的坐标分别为(20,0),(20,10).P、Q分别为线段OB、OA上的动点,当PQ+PA最小时,点P的坐标为(12,6).
已知在平面直角坐标系中,矩形OABC的顶点O为坐标原点,顶点A、B的坐标分别为(20,0),(20,10).P、Q分别为线段OB、OA上的动点,当PQ+PA最小时,点P的坐标为(12,6).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 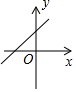 | B. | 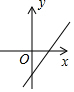 | C. | 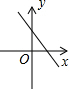 | D. | 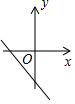 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com