
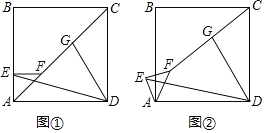
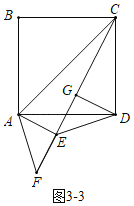
����Ŀ����ͼ���ı���ABCDΪ�����Σ���AEFΪ����ֱ�������Σ���AEF��90�㣬����FC��GΪFC���е㣬����GD��ED��
��1����ͼ����E��AB�ϣ�ֱ��д��ED��GD��������ϵ��
��2����ͼ���еġ�AEF�Ƶ�A��ʱ����ת�������������䣬��ͼ������1���еĽ����Ƿ������˵�����ɣ�
��3����AB��5��AE��1����ͼ���еġ�AEF�Ƶ�A��ʱ����תһ�ܣ���E��F��C���㹲��ʱ��ֱ��д��ED�ij���
���𰸡���1��DE��![]() DG����2�����������ɼ���������3��DE�ij�Ϊ4
DG����2�����������ɼ���������3��DE�ij�Ϊ4![]() ��3
��3![]() ��
��
��������
��1������������ۣ�DE=![]() DG����ͼ1�У�����EG���ӳ�EG��BC���ӳ�����M������DM��֤����CMG�ա�FEG��AAS�����Ƴ�EF=CM��GM=GE����֤����DCM�ա�DAE��SAS�����ɽ�����⣻
DG����ͼ1�У�����EG���ӳ�EG��BC���ӳ�����M������DM��֤����CMG�ա�FEG��AAS�����Ƴ�EF=CM��GM=GE����֤����DCM�ա�DAE��SAS�����ɽ�����⣻
��2����ͼ2�У����۳���������EG���ӳ�EG��M��ʹ��GM=GE������CM��DM���ӳ�EF��CD��R����֤���������ƣ�
��3����������������Σ�����ͼ3-1�У���E��F��C����ʱ������ͼ3-3�У���E��F��C����ʱ���ֱ���⼴�ɣ�
�⣺��1�����ۣ�DE��![]() DG��
DG��
���ɣ���ͼ1�У�����EG���ӳ�EG��BC���ӳ�����M������DM��
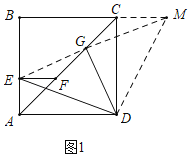
���ı���ABCD�������Σ�
��AD��CD����B����ADC����DAE����DCB����DCM��90����
�ߡ�AEF����B��90����
��EF��CM��
���CMG����FEG��
�ߡ�CGM����EGF��GC��GF��
���CMG�ա�FEG��AAS����
��EF��CM��GM��GE��
��AE��EF��
��AE��CM��
���DCM�ա�DAE��SAS����
��DE��DM����ADE����CDM��
���EDM����ADC��90����
��DG��EM��DG��GE��GM��
���EGD�ǵ���ֱ�������Σ�
��DE��![]() DG��
DG��
��2����ͼ2�У����۳�����
���ɣ�����EG���ӳ�EG��M��ʹ��GM��GE������CM��DM���ӳ�EF��CD��R��
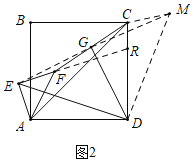
��EG��GM��FG��GC����EGF����CGM��
���CGM�ա�FGE��SAS����
��CM��EF����CMG����GEF��
��CM��ER��
���DCM����ERC��
�ߡ�AER+��ADR��180����
���EAD+��ERD��180����
�ߡ�ERD+��ERC��180����
���DCM����EAD��
��AE��EF��
��AE��CM��
���DAE�ա�DCM��SAS����
��DE��DM����ADE����CDM��
���EDM����ADC��90����
��EG��GM��
��DG��EG��GM��
���EDG�ǵ���ֱ�������Σ�
��DE��![]() DG��
DG��
��3������ͼ3��1�У���E��F��C����ʱ��
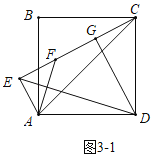
��Rt��ADC��AC��![]() ��
��![]() ��5
��5![]() ��
��
��Rt��AEC��EC��![]() ��
��![]() ��7��
��7��
��CF��CE��EF��6��
��CG��![]() CF��3��
CF��3��
�ߡ�DGC��90����
��DG��![]() ��
��![]() ��4��
��4��
��DE��![]() DG��4
DG��4![]() ��
��
����ͼ3��3�У���E��F��C����ʱ��ͬ���ɵ�DE��3![]() ��
��
����������DE�ij�Ϊ4![]() ��3
��3![]() ��
��


 һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�
һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() ��
��![]() ��1������
��1������![]() ��
��![]() ��
��![]() ��������
��������![]() ����
����![]() ��ͼ��Ľ���.
��ͼ��Ľ���.
��1����![]() ��
��
��2��������![]() ��ͼ����
��ͼ����![]() ��ֻ��һ�����㣬��
��ֻ��һ�����㣬��![]() ��
��![]() ��
��
��3����![]() ���赱
���赱![]() ʱ������
ʱ������![]() �����ֵΪ
�����ֵΪ![]() ����СֵΪ
����СֵΪ![]() ����
����![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+bx+c�ĶԳ���Ϊֱ��x��1���ҹ��㣨3��0�������н��ۣ���abc��0����a��b+c��0����2a+b��0����b2��4ac��0����ȷ���У�����������
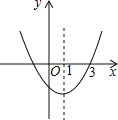
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
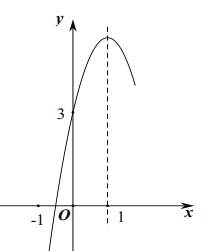
����Ŀ����ͼ��ʾ��������![]() �ĶԳ���Ϊֱ��
�ĶԳ���Ϊֱ��![]() ����
����![]() ���һ����������Ϊ
���һ����������Ϊ![]() ���䲿��ͼ����ͼ��ʾ�����н���:
���䲿��ͼ����ͼ��ʾ�����н���:
��![]() ��
��
��![]() ��
��
�۷���![]() ����������
����������![]() ��
��
�ܷ���![]() ��һ��ʵ������
��һ��ʵ������![]() ��
��
�ݵ�![]() ʱ��
ʱ��![]() ��
��![]() ���������.
���������.
���н�����ȷ�ĸ�����( )
A.![]() ��B.
��B.![]() ��C.
��C.![]() ��D.
��D.![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������п��忼ʱ��Խ��Խ�����꼶���˽�����꼶1000��ѧ����ĩ�ڼ�����������������ڳ����꼶�����ȡ��20��������20��Ů������������ĩ�ڼҵĶ���ʱ������˵��飬���ռ��õ����������ݣ���λ��min����
������20 30 40 45 60 120 80 50 100 45 85 90 90 70 90 50 90 50 70 40
����75 30 120 70 60 100 90 40 75 60 75 75 80 90 70 80 50 80 100 90
ͳ�����ݣ�������������ͳ�Ʊ���
ʱ�� x | x��30 | 30��x��60 | 60��x��90 | 90��x��120 | |
���� | 2 | 8 | 8 | 2 | |
�� | 1 | m | n | 3 |
�������ݣ��������ݵļ��ƽ��������λ�����������±���ʾ
���� | ƽ���� | ��λ�� | ���� | |
���� | a | 65.75 | b | 90 |
�� | c | 75.5 | 75 | d |
��1���뽫����ı���������m�� ��n�� ��a�� ��b�� ��c�� ��d��
��2����֪���꼶��Ů��������࣬���ݵ�������ݣ����Ƴ����꼶��ĩ�ڼҶ�����ʱ���� 90min ���ϵ�ͬѧԼ�ж����ˣ�
��3������ʦ���˱������ݺ���Ϊ�����꼶��Ů����ĩ�������ñ������ã�������ͳ�����ݣ�д������֧������ʦ�۵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ:����ABC��,��ABC=90��,AB=BC=8cm,����P�ӵ�A����,��2cm/s���ٶ�������AB�˶�,ͬʱ����Q�ӵ�C����,��2cm/s���ٶ��ر�BC���ӳ����˶�,PQ��ֱ��AC�ཻ�ڵ�D����P���˶�ʱ��Ϊt��,��PCQ�����ΪS cm2��
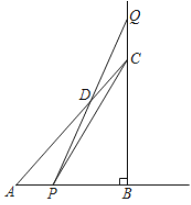
(1)ֱ��д��AC�ij�:AC= cm��
(2)���S����t�ĺ�����ϵʽ,���������P�˶�����ʱ,S��PCQ=S��ABC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���x2����m��2��x����2m��1��=0��
��1����֤�����̺�����������ȵ�ʵ������
��2�����˷��̵�һ������1����������̵���һ�����������Դ�����Ϊ�߳���ֱ�������ε��ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
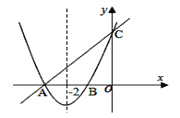
����Ŀ����֪����������ֱ��y=x+3�ֱ���x���y����ͬһ�㣬����ֱ��ǵ�A�͵�C���������ߵĶԳ���Ϊֱ��x=-2��
��1�������������x�����������A��B�����꣮
��2����ȷ�������ߵĽ���ʽ��
��3���۲�ͼ����ֱ��д�����κ���ֵС��һ�κ���ֵ���Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ![]() ���ڵ������������ȳ�������AB��CD������֮��������һ����������״�����ӣ�����ͼ�е�ֱ������ϵ���������ӿ�����
���ڵ������������ȳ�������AB��CD������֮��������һ����������״�����ӣ�����ͼ�е�ֱ������ϵ���������ӿ�����![]() ��ʾ
��ʾ
![]() ������������͵������ľ��룻
������������͵������ľ��룻
![]() ������ʵ����Ҫ��Ҫ����������֮���ټ�һ������EF�����ӽ���֧��
������ʵ����Ҫ��Ҫ����������֮���ټ�һ������EF�����ӽ���֧��![]() ��ͼ
��ͼ![]() ����֪����EF��AB����Ϊ3m�����Ե�����Ҳ����������״��������EF������ӵ���͵㵽EF�ľ���Ϊ1m��������ľ���Ϊ1.8m��������EF�ij���
����֪����EF��AB����Ϊ3m�����Ե�����Ҳ����������״��������EF������ӵ���͵㵽EF�ľ���Ϊ1m��������ľ���Ϊ1.8m��������EF�ij���
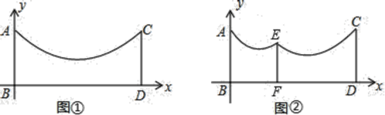
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com