
【题目】如图,在△ABC中,∠ACB=90°,AB=10,AC=6.动点P从点A出发,沿折线AC﹣CB运动,在边AC上以每秒3个单位长度的速度运动,在边BC上以每秒4个单位长度的速度运动,到点B停止,当点P不与△ABC的顶点重合时,过点P作其所在直角边的垂线交AB于点Q;以Q为直角顶点向PQ右侧作Rt△PQD,且QD=![]() PQ.设△PQD与△ABC重叠部分图形的面积为S,点P运动的时间为t(s).
PQ.设△PQD与△ABC重叠部分图形的面积为S,点P运动的时间为t(s).
(1)当点P在边AC上时,求PQ的长(含t的代数式表示);
(2)点D落在边BC上时,求t的值;
(3)求S与t之间的函数关系式;
(4)设PD的中点为E,作直线CE.当直线CE将△PQD的面积分成1:5两部分时,直接写出t的值.

【答案】(1)PQ=4t;(2)t=![]() ;(3)S=
;(3)S=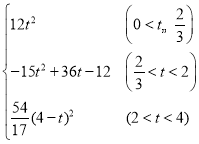 ;(4)
;(4)![]() 或
或![]() .
.
【解析】
(1)由PQ∥BC,推出△APQ∽△ACB,可得 ![]() ,由此构建关系式即可解决问题.
,由此构建关系式即可解决问题.
(2)当点D落在BC上时,四边形PCDQ是矩形,根据PC=DQ,构建方程解决问题即可.
(3)分三种情形:①如图3﹣1中,当0<t≤![]() 时,重叠部分是△PQD.②如图3﹣2中,当
时,重叠部分是△PQD.②如图3﹣2中,当![]() <t<2时,重叠部分是四边形PQMN.③如图3﹣3中,当2<t<4时,重叠部分是△PQN,分别求解即可.
<t<2时,重叠部分是四边形PQMN.③如图3﹣3中,当2<t<4时,重叠部分是△PQN,分别求解即可.
(4)分两种情形:①如图4﹣1中,设直线CE交DQ于N,连接OE.当QN=2DN时,直线CE将△PQD的面积分成1:5两部分.②如图4﹣2中,如图4﹣2中,设直线CE交PQ于N,连接OE,延长QD交CE于M.当QN=2PN时,直线CE将△PQD的面积分成1:5两部分,分别求解即可.
解:(1)如图1中,当点P在AC上时,

在Rt△ABC中,∵∠C=90°,AB=10,AC=6,
∴BC=![]() =8.
=8.
∵PQ∥BC,∴△APQ∽△ACB,
∴![]() ,
,
∴![]() ,
,
∴PQ=4t.
(2)当点D落在BC上时,四边形PCDQ是矩形,∴PC=DQ.
∵PQ=4t,DQ=![]() PQ,
PQ,
∴DQ=6t,
∴6﹣3t=6t,
解得:t=![]() .
.
(3)①如图3﹣1中,当0<t≤![]() 时,重叠部分是△PQD.
时,重叠部分是△PQD.
S=![]() PQDQ=
PQDQ=×4t×6t=12t2.

②如图3﹣2中,当![]() <t<2时,重叠部分是四边形PQMN,
<t<2时,重叠部分是四边形PQMN,
S=S△PQD﹣S△DMN=12t2﹣![]() ×(9t﹣6)×
×(9t﹣6)×![]() (9t﹣6)=﹣15t2+36t﹣12.
(9t﹣6)=﹣15t2+36t﹣12.

③如图3﹣3中,当2<t<4时,重叠部分是△PQN,

由题意PC=4(t﹣2),PB=BC﹣PC=16﹣4t=4(4﹣t),
∴PQ=3(4﹣t),DQ=![]() (4﹣t).
(4﹣t).
∵PB∥DQ,∴PN:DN=PB:DQ=8:9,
∴S=![]() S△PQD=
S△PQD=![]()
![]() 3(4﹣t)
3(4﹣t)![]() (4﹣t)=
(4﹣t)=![]() (4﹣t)2.
(4﹣t)2.
综上所述: .
.
(4)①如图4﹣1中,设直线CE交DQ于N,连接OE.

当QN=2DN时,直线CE将△PQD的面积分成1:5两部分.
∵PE=DE,PC∥DN,
∴![]() ,∴PC=DN,
,∴PC=DN,
∴QN=2PC,DQ=3PC,
∴6t=3(6﹣3t),
∴t=![]() .
.
②如图4﹣2中,如图4﹣2中,设直线CE交PQ于N,连接OE,延长QD交CE于M.

当QN=2PN时,直线CE将△PQD的面积分成1:5两部分.
∵PC∥QM,PE=ED,
∴![]() ,
,![]() ,
,
∴PC=DM=4(t﹣2),QM=2PC,
∴![]() (4﹣t)+4(t﹣2)=2×4(t﹣2),
(4﹣t)+4(t﹣2)=2×4(t﹣2),
解得:t=![]() ,
,
综上所述:满足条件的t的值为![]() 或
或![]() .
.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:
【题目】如图在直角坐标系中△ABC的顶点A、B、C三点坐标为A(7,1),B(8,2),C(9,0).
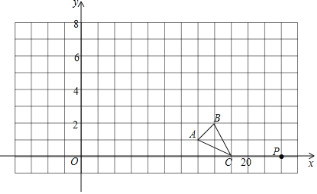
(1)请在图中画出△ABC的一个以点P(12,0)为位似中心,相似比为3的位似图形△A'B'C'(要求与△ABC在P点同一侧);
(2)直接写出A'点的坐标;
(3)直接写出△A'B'C'的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过学习锐角三角比,我们知道在直角三角形中,一个锐角的大小与两条边长的比值是一一对应的,因此,两条边长的比值与角的大小之间可以相互转化。类似的,可以在等腰三角形中建立边角之间的联系。我们定义:等腰三角形中底边与腰的比叫做底角的邻对(can).

如图(1)在△![]() 中,
中,![]() ,底角
,底角![]() 的邻对记作
的邻对记作![]() ,这时
,这时![]() ,容易知道一个角的大小与这个角的邻对值也是一一对应的.根据上述角的邻对的定义解下列问题:
,容易知道一个角的大小与这个角的邻对值也是一一对应的.根据上述角的邻对的定义解下列问题:
(1)![]() = ;
= ;
(2)如图(2),在△![]() 中,
中,![]() ,
,![]() ,
,![]() ,求△
,求△![]() 的周长
的周长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,我国海关总署严厉打击“洋垃圾”违法行动,坚决把“洋垃圾”拒于国门之外如图,某天我国一艘海监船巡航到![]() 港口正西方的
港口正西方的![]() 处时,发现在
处时,发现在![]() 的北偏东
的北偏东![]() 方向,相距
方向,相距![]() 海里处的
海里处的![]() 点有一可疑船只正沿
点有一可疑船只正沿![]() 方向行驶,
方向行驶,![]() 点在
点在![]() 港口的北偏东
港口的北偏东![]() 方向上,海监船向
方向上,海监船向![]() 港口发出指令,执法船立即从
港口发出指令,执法船立即从![]() 港口沿
港口沿![]() 方向驶出,在
方向驶出,在![]() 处成功拦截可疑船只,此时
处成功拦截可疑船只,此时![]() 点与
点与![]() 点的距离为
点的距离为![]() 海里.
海里.
(1)求![]() 的度数与
的度数与![]() 点到直线
点到直线![]() 的距离;
的距离;
(2)执法船从![]() 到
到![]() 航行了多少海里?(结果保留根号)
航行了多少海里?(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
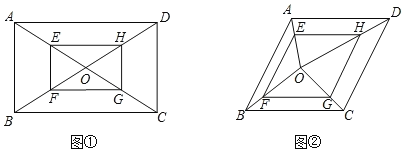
【题目】(教材呈现)
下图是华师版九年级上册数学教材第79页的部分内容.

请根据教材内容,结合图①,写出完整的解题过程.
(结论应用)
(1)在图①中,若AB=2,∠AOD=120°,则四边形EFGH的面积为______.
(2)如图②,在菱形ABCD中,∠BAD=120°,O是其内任意一点,连接O与菱形ABCD各顶点,四边形EFGH的顶点E、F、G、H分别在AO、BO、CO、DO上,EO=2AE,EF∥AB∥GH,且EF=GH,若△EFO与△GHO的面积和为![]() ,则菱形ABCD的周长为______.
,则菱形ABCD的周长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
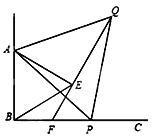
【题目】如图, 已知∠ABC=90°,点P为射线BC上任意一点(点P与点B不重合),分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连接QE并延长交BP于点F. 试说明:(1)△ABP≌△AEQ;(2)EF=BF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组织七年级学生进行“垃圾分类”知识测试,现随机抽取部分学生的成绩进行统计,并绘制如下频数分布表以及频数分布直方图.
分数档 | 分数段/分 | 频数 | 频率 |
A | 90<x≤100 | a | 0.12 |
B | 80<x≤90 | b | 0.18 |
C | 70<x≤80 | 20 | c |
D | 60<x≤70 | 15 | d |
请根据以上信息,解答下列问题:
(1)已知A,B档的学生人数之和等于D档学生人数,求被抽取的学生人数,并把频数分布直方图补充完整.
(2)该校七年级共有200名学生参加测试,请估计七年级成绩在C档的学生人数.
(3)你能确定被抽取的这些学生的成绩的众数在哪一档吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.

(1)若△BPQ与△ABC相似,求t的值;
(2)试探究t为何值时,△BPQ的面积是![]() cm2;
cm2;
(3)直接写出t为何值时,△BPQ是等腰三角形;
(4)连接AQ,CP,若AQ⊥CP,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点
经过点![]() ,交y 轴于点C:
,交y 轴于点C:
(1)求抛物线的顶点坐标.
(2)点![]() 为抛物线上一点,是否存在点
为抛物线上一点,是否存在点![]() 使
使![]() ,若存在请直接给出点
,若存在请直接给出点![]() 坐标;若不存在请说明理由.
坐标;若不存在请说明理由.
(3)将直线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,与抛物线交于另一点
,与抛物线交于另一点![]() ,求直线
,求直线![]() 的解析式.
的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com