【题目】点E在射线OA上，点F在射线OB 上，AO⊥BO，EM平分∠AEF，FM平分∠BFE，则tan∠EMF的值为( )
A.
B.
C.1D.
【答案】C
【解析】
根据三角形外角的性质求得∠AEF+∠BFE=270°，由角平分线定义可求得∠MEF+∠MFE=135°，根据三角形内角和定理可求出∠EMF=45°，从而可得出结论．
如图，
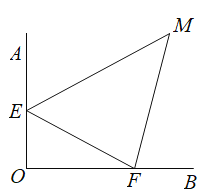
∵AO⊥BO
∴∠AOB=90°
∴∠OEF+∠OFE=90°
∵∠AEF和∠BFE是△EOF的外角
∴∠AEF=90°+∠OFE，∠BFE=90°+∠OEF
∴∠AEF+∠BFE=90°+90°+∠OFE+∠OEF=270°
∵EM平分∠AEF，FM平分∠BFE，
∴∠MEF+∠MFE=
(∠AEF+∠BFE) =135°，
∵∠MEF+∠MFE+∠M=180°
∴∠M=180°-(∠MEF+∠MFE)=180°-135°=45°
∴tan∠EMF=tan45°=1
故选：C．
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目：初中数学 来源： 题型：
【题目】如图，△ABC中，∠ACB=90°，∠BAC=20°，点O是AB的中点，将OB绕点O顺时针旋转α角时（0°＜α＜180°），得到OP，当△ACP为等腰三角形时，α的值为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某口罩加工厂有
两组工人共
人，
组工人每人每小时可加工口罩
只，
组工人每人每小时可加工口罩
只，两组工人每小时一共可加工口罩
只．
（1）求两组工人各多少人；
（2）由于疫情加重两组工人均提高了工作效率，一名组工人和一名组工人每小时共可生产口罩
只，若两组工人每小时至少加工
只口罩，那么组工人每人每小时至少加工多少只口罩？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，反比例函数
的图像经过点
，点
，连接
，
，若
．
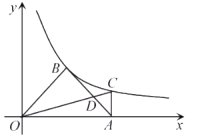
（1）求反比例函数的解析式；
（2）过点
作
轴，交反比例函数的图像于点
，连接
，与交于点
，求
的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，D为⊙O上一点，点C在直径BA的延长线上，且∠CDA＝∠CBD．
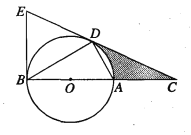
（1）求证：CD是⊙O的切线；
（2）若⊙O的半径为1，∠CBD＝30°，则图中阴影部分的面积；
（3）过点B作⊙O的切线交CD的延长线于点E若BC＝12，tan∠CDA＝
，求BE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一次函数y＝k1x+b的图象与反比例函数y＝
的图象相交于A、B两点，其中点A的坐标为（﹣1，4），点B的坐标为（4，n）．
（1）求这两个函数的表达式；
（2）根据图象，直接写出满足k1x+b＞的x的取值范围．
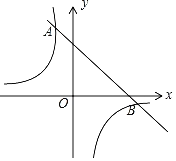
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙两地相距300千米，一辆货车和一辆轿车先后从甲地出发驶向乙地，如图，线段OA表示货车离甲地距离y（千米）与时间x（小时）之间的函数关系；折线OBCDA表示轿车离甲地距离y（千米）与时间x（小时）之间的函数关系．请根据图象解答下列问题：
（1）当轿车刚到乙地时，此时货车距离乙地 千米；
（2）当轿车与货车相遇时，求此时x的值；
（3）在两车行驶过程中，当轿车与货车相距20千米时，求x的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
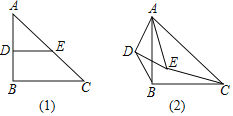
【题目】如图1，在Rt△ABC中，∠ABC＝90°，AB＝BC＝4，点D、E分别是边AB、AC的中点，连接DE，将△ADE绕点A按顺时针方向旋转，记旋转角为α，BD、CE所在直线相交所成的锐角为β．
(1)问题发现当α＝0°时，
＝_____；β＝_____°．
(2)拓展探究
试判断：当0°≤α＜360°时，和β的大小有无变化？请仅就图2的情形给出证明．
(3)在△ADE旋转过程中，当DE∥AC时，直接写出此时△CBE的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】以下是通过折叠正方形纸片得到等边三角形的步骤取一张正方形的纸片进行折叠，具体操作过程如下：
第一步：如图，先把正方形ABCD对折，折痕为MN；
第二步：点E在线段MD上，将△ECD沿EC翻折，点D恰好落在MN上，记为点P，连接BP可得△BCP是等边三角形
问题：在折叠过程中，可以得到PB=PC；依据是________________________.
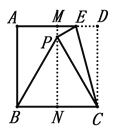
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com