
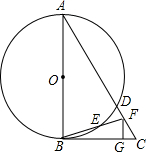
 如图,以△ABC边AB为直径的⊙O交AC于点D,点F在DC上,BF交⊙O于点E,BE=EF,∠BAC=2∠CBF,CG⊥BF于点G.
如图,以△ABC边AB为直径的⊙O交AC于点D,点F在DC上,BF交⊙O于点E,BE=EF,∠BAC=2∠CBF,CG⊥BF于点G.分析 (1)连接AE,根据圆周角定理求得∠AEB=90°,然后根据垂直平分线的性质求得AB=AF,根据等腰三角形三线合一的性质求得∠BAE=∠FAE=$\frac{1}{2}$∠BAC,从而求得∠BAE=∠FAE=$\frac{1}{2}$∠BAC,即可求得∠BAE+∠ABF=∠CBF+∠ABF=90°,即可证得结论;
(2)根据已知求得CF=4,设AB=AF=x,z则AC=x+4,通过∠C的正弦函数即可求得AB,继而求得⊙O的半径.
解答  (1)证明:连接AE,
(1)证明:连接AE,
∵AB是直径,
∴∠AEB=90°,
∵BE=EF,
∴AB=AF,
∴∠BAE=∠FAE=$\frac{1}{2}$∠BAC,
∵∠BAC=2∠CBF,
∴∠BAE=∠CBF,
∴∠BAE+∠ABF=∠CBF+∠ABF=90°,
即∠ABC=90°,
∴BC是⊙O的切线;
(2)解:∵FG⊥BC,∠C=60°,
∴∠CFG=30°,
∴CF=2CG=4,
∵AF=AB,
设AB=AF=x,z则AC=x+4,
∵∠C=60°,
∴sin∠C=$\frac{AB}{AC}$,
∴$\frac{\sqrt{3}}{2}$=$\frac{x}{x+4}$,解得x=8$\sqrt{3}$+12,
∴AB=8$\sqrt{3}$+12,
∴⊙O的半径为(4$\sqrt{3}$+6).
点评 本题考查了圆周角定理,等腰三角形的判定和性质,切线的判定,直角三角函数等,作出辅助线构建直角三角形是解题的关键.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:选择题
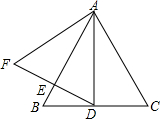 如图,等腰三角形ABC中,AB=AC,∠BAC=70°,D是BC中点,DE⊥AB于E,延长DE至F,使EF=DE,则∠F的度数是( )
如图,等腰三角形ABC中,AB=AC,∠BAC=70°,D是BC中点,DE⊥AB于E,延长DE至F,使EF=DE,则∠F的度数是( )| A. | 30° | B. | 35° | C. | 55° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明将我市交通部门在某雷达测速区监测到的一组汽车的时速数据进行收集、整理,制作成如下不完整的统计图表,根据提供的信息解答下列问题:
小明将我市交通部门在某雷达测速区监测到的一组汽车的时速数据进行收集、整理,制作成如下不完整的统计图表,根据提供的信息解答下列问题:| 时速x(km/h) | 频 数 | 频 率 |
| 30≤x≤40 | 10 | 0.05 |
| 40≤x≤50 | 36 | 0.18 |
| 50≤x≤60 | 78 | 0.39 |
| 60≤x≤70 | 56 | 0.28 |
| 70≤x≤80 | 20 | 0.10 |
| 总 计 | 200 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,从矩形ABCD的一个顶点C向对角线BD作垂线CE,垂足是E,若BE=3DE,两对角线的交点O至BC的距离OF=36cm,求AC的长.
如图,从矩形ABCD的一个顶点C向对角线BD作垂线CE,垂足是E,若BE=3DE,两对角线的交点O至BC的距离OF=36cm,求AC的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 实数x在数轴上位置如图,则x0,x-1,x-2,x-4的大小关系为( )
实数x在数轴上位置如图,则x0,x-1,x-2,x-4的大小关系为( )| A. | x0>x-1>x-2>x-4 | B. | x-4>x-2>x-1>x0 | C. | x-2>x-4>x0>x-1 | D. | x0>x-2>x-4>x-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com