
【题目】如图,![]() 中,以
中,以![]() ,以
,以![]() 为边作等腰三角形
为边作等腰三角形![]() ,
,![]() ,
,![]() ,
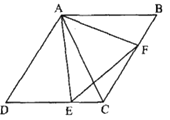
,![]() 分别为边CD,BC上的点,连结AE,AF,EF,
分别为边CD,BC上的点,连结AE,AF,EF,![]() .
.
![]() 求证:
求证:![]() .
.
![]() 若
若![]() ,求
,求![]() 的度数.
的度数.
![]() 请直接指出:当
请直接指出:当![]() 点在
点在![]() 何处时,
何处时,![]() ?
?
【答案】(1)证明见解析;(2)![]() ;(3)当
;(3)当![]() 为
为![]() 中点时,
中点时,![]() ,理由见解析.
,理由见解析.
【解析】
(1)利用角的和差关系可得∠EAC=∠BAF,根据等腰三角形的性质可得∠ACD=∠B=60°,利用ASA即可证明△ABF≌△ACE;(2)由△ABF≌△ACE可得AE=AF,∠AEC=∠AFB,根据平角定义可得![]() ,根据等腰三角形的性质可求出∠AEF=60°,即可求出∠EFC的度数;(3)根据全等三角形的性质可得AE=AF,CE=BF,由等腰三角形的性质可得AC是EF的垂直平分线,即可得CE=CF,进而可得CF=BF,即可得点F为BC中点.
,根据等腰三角形的性质可求出∠AEF=60°,即可求出∠EFC的度数;(3)根据全等三角形的性质可得AE=AF,CE=BF,由等腰三角形的性质可得AC是EF的垂直平分线,即可得CE=CF,进而可得CF=BF,即可得点F为BC中点.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在△ABF和△ACE中, ,
,
![]() .
.
![]() 由
由![]() 可知,
可知,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.

![]() 当
当![]() 为
为![]() 中点时,
中点时,![]() ,理由如下:
,理由如下:
![]() ,
,
![]() ,
,
∵AC⊥EF,
∴AC为EF的垂直平分线,
∴CE=CF,
∴BF=CF,即点F为BC中点.


科目:初中数学 来源: 题型:
【题目】饮水机接通电源就进入自动程序,若在水温为![]() 时,接通电源后,水温
时,接通电源后,水温![]() 和时间
和时间![]() 的关系如图.开机加热时每分钟上升
的关系如图.开机加热时每分钟上升![]() ,加热到
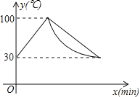
,加热到![]() ,饮水机关机停止加热,水温开始下降,下降时水温与开机后的时间成反比例关系.当水温降至
,饮水机关机停止加热,水温开始下降,下降时水温与开机后的时间成反比例关系.当水温降至![]() ,饮水机自动开机,重复上述自动程序.若上午
,饮水机自动开机,重复上述自动程序.若上午![]() 开机,则
开机,则![]() 时能否喝到超过
时能否喝到超过![]() 的水?说明理由.
的水?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )

A.角平分线上的点到这个角两边的距离相等
B.角的内部到角的两边的距离相等的点在角的平分线上
C.三角形三条角平分线的交点到三条边的距离相等
D.以上均不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC与△A'B'C在平面直角坐标系中的位置如图.

(1)分别写出B、B'的坐标:B______;B′______;
(2)若点P(a,b)是△ABC内部一点,则平移后△A'B'C内的对应点P′的坐标为______;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
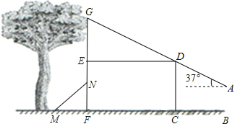
【题目】身高![]() 米的兵兵在建筑物前放风筝,风筝不小心挂在了树上.在如图所示的平面图形中,矩形
米的兵兵在建筑物前放风筝,风筝不小心挂在了树上.在如图所示的平面图形中,矩形![]() 代表建筑物,兵兵位于建筑物前点
代表建筑物,兵兵位于建筑物前点![]() 处,风筝挂在建筑物上方的树枝点
处,风筝挂在建筑物上方的树枝点![]() 处(点
处(点![]() 在
在![]() 的延长线上).经测量,兵兵与建筑物的距离
的延长线上).经测量,兵兵与建筑物的距离![]() 米,建筑物底部宽
米,建筑物底部宽![]() 米,风筝所在点
米,风筝所在点![]() 与建筑物顶点
与建筑物顶点![]() 及风筝线在手中的点
及风筝线在手中的点![]() 在同一条直线上,点
在同一条直线上,点![]() 距地面的高度
距地面的高度![]() 米,风筝线与水平线夹角为
米,风筝线与水平线夹角为![]() .
.
![]() 求风筝距地面的高度
求风筝距地面的高度![]() ;
;
![]() 在建筑物后面有长
在建筑物后面有长![]() 米的梯子
米的梯子![]() ,梯脚
,梯脚![]() 在距墙
在距墙![]() 米处固定摆放,通过计算说明:若兵兵充分利用梯子和一根
米处固定摆放,通过计算说明:若兵兵充分利用梯子和一根![]() 米长的竹竿能否触到挂在树上的风筝?
米长的竹竿能否触到挂在树上的风筝?
(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的中线,E、F分别是AD和AD延长线上的点,且DE=DF,连结BF,CE.下列说法:①△ABD和△ACD面积相等;②CE=AE;③△BDF≌△CDE; ④BF∥CE;⑤∠BAD=∠CAD.其中正确的有( ).

A.①⑤B.③⑤C.①③④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,a,b,c分别是∠A、∠B、∠C的对边
(1)若a=![]() ,c=4,求b
,c=4,求b
(2)若c=8,∠A=30°,求b
(3)若a:b=3:4,c=15,求Rt△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为菱形ABCD对角线的交点,M是射线CA上的一个动点(点M与点C、O、A都不重合),过点A、C分别向直线BM作垂线段,垂足分别为E、F,连接OE,OF.


(1)①依据题意补全图形;
②猜想OE与OF的数量关系为_________________.
(2)小东通过观察、实验发现点M在射线CA上运动时,(1)中的猜想始终成立.
小东把这个发现与同学们进行交流,通过讨论,形成了证明(1)中猜想的几种想法:
想法1:由已知条件和菱形对角线互相平分,可以构造与△OAE全等的三角形,从而得到相等的线段,再依据直角三角形斜边中线的性质,即可证明猜想;
想法2:由已知条件和菱形对角线互相垂直,能找到两组共斜边的直角三角形,例如其中的一组△OAB和△EAB,再依据直角三角形斜边中线的性质,菱形四边相等,可以构造一对以OE和OF为对应边的全等三角形,即可证明猜想.
……
请你参考上面的想法,帮助小东证明(1)中的猜想(一种方法即可).
(3)当∠ADC=120°时,请直接写出线段CF,AE,EF之间的数量关系是_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学研究课上,老师带领大家探究《折纸中的数学问题》时,出示如图1所示的长方形纸条![]() ,其中
,其中![]() ,
,![]() .然后在纸条上任意画一条截线段
.然后在纸条上任意画一条截线段![]() ,将纸片沿
,将纸片沿![]() 折叠,
折叠,![]() 与
与![]() 交于点
交于点![]() ,得到
,得到![]() .如图2所示:
.如图2所示:

探究:
(1)若![]() ,
,![]() ______°;
______°;
(2)改变折痕![]() 位置,
位置,![]() 始终是______三角形,请说明理由;
始终是______三角形,请说明理由;
应用:
(3)爱动脑筋的小明在研究![]() 的面积时,发现
的面积时,发现![]() 边上的高始终是个不变的值.根据这一发现,他很快研究出
边上的高始终是个不变的值.根据这一发现,他很快研究出![]() 的面积最小值为
的面积最小值为![]() ,此时
,此时![]() 的大小可以为______°;
的大小可以为______°;
(4)小明继续动手操作,发现了![]() 面积的最大值.请你求出这个最大值.
面积的最大值.请你求出这个最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com