Question

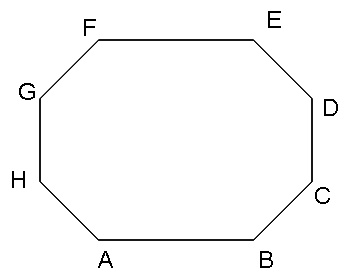
如图，一个凸八边形ABCDEFGH，8个内角都相等，边AB、BC、CD、DE、FG的长分别为7、4、2、5、6、2，求该八边形的周长．

Answer 1

答案：略
解析：

双向延长AB、CD、EF、GH．分别相交于M、N、P、Q，得到四边形MNPQ．因为凸八边形8个内角都相等，所以每一个内角为180°×(8－2)÷8=135°，所以∠AHN=∠HAN=∠BCP=∠CBP=∠QDE=∠QED=∠MFG=∠MGF=180°－135°=45°． 所以∠ANH=∠BPC=∠DQE=∠FMG=90°，△ANH、△BPC、△DQE、△FMG都是等腰直角三角形． 设GH=x，HA=y，由MQ=NP，得MF＋FE＋EQ=NA＋AB＋BP，即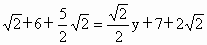， 所以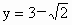． 由MN=PQ．得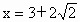， 所以该八边形的周长为．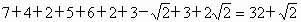

提示：

这道题让同学们学会适当添加辅助线，将多边形转化为熟悉的几何图形，利用其性质，并通过计算或列方程等方法把几何问题代数化，这也是解决问题的常用方法．