练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，长方体的高为8cm，底面是正方形，边长为3cm，现有绳子从A出发，沿长方体表面到达C处，则绳子的最短长度是（　　）
    A、8B、9C、10D、11
    考点：平面展开-最短路径问题
    专题：
    分析：把长方体右边的表面展开，连接AC，则AC就是绳子的最短时经过的路径，然后根据勾股定理求解．
    解答：解：如图所示，将长方体右边的表面翻折90°（展开），
    连接AC，显然两点之间线段最短，AC为点A到点C的最短距离，
    由勾股定理知：AC2=82+（3+3）2=100，AC=10cm．
    即绳子最短为10cm．
    故选：C．
    点评：本题是勾股定理的应用，还利用了两点之间线段最短的性质．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

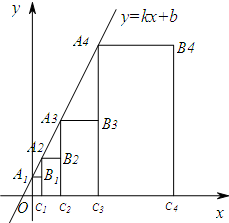    矩形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图所示放置．点A1，A2，A3，A4…和点C1，C2，C3，C4…，分别在直线y=kx+b（k＞0）和x轴上，若点B1（1，2），B2（3，4），且满足
    A1A2
    A2A3
    =
    A2A3
    A3A4
    =
    A3A4
    A4A5
    =…=
    An-1An
    AnAn-1
    ，则直线y=kx+b的解析式为
     
    ，点B3的坐标为
     
    ，点Bn的坐标为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    若关于x的不等式kx2+（k-6）x+2＞0的解为全体实数，则实数k的取值范围是（　　）
    A、-2＜k＜18
    B、-18＜k＜-2
    C、2＜k＜18
    D、-18＜k＜2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，设正方体ABCD-A1B1C1D1的棱长为1，黑、白两个甲壳虫同时从A点出发，以相同的速度分别沿棱向前爬行，黑甲壳虫爬行的路线是AA1→A1D1→…，白甲壳虫爬行的路线是AB→BB1→…，并且都遵循如下规则：所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交（其中n是正整数）．那么当黑、白两个甲壳虫各爬行完第2013条棱分别停止在所到的正方体顶点处时，它们之间的距离是（　　）
    A、0
    B、1
    C、
    		2
    D、
    		3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    下列式子中，是二次根式的是（　　）
    A、
    		7
    B、
    37
    C、
    		-5
    D、-5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    将矩形ABCD沿BE折叠，得到如图所示的图形，已知∠CBA′=34°，则∠AEB的大小是（　　）
    A、34°B、56°
    C、28°D、62°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    建立两个适当的平面直角坐标系，分别表示边长为8的正方形的顶点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如果二次函数y=x2-x+c的图象过点（1，2）
    （1）求这个二次函数的解析式，
    （2）求该抛物线的顶点坐标，并写出该函数图象的对称轴．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，△ABC的角平分线BO、CO交于点O，OE∥AB，OF∥AC，BC=10，①△OEF的周长=
     
    ；②说明你的理由．

    查看答案和解析>>

    同步练习册答案