
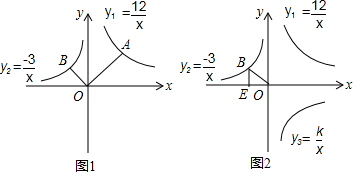
分析 (1)设A(a,b),根据反比例函数图象上点的坐标特征,得出ab=12,进而得出a=b=2$\sqrt{3}$,就可求得A的坐标;
(2)过A、B分别作y轴的垂线,垂足为C、D,通过证得△AOC∽△OBD,然后根据相似三角形的性质即可求得;
(3)分四种情况分别讨论求得.
解答  解:(1)设A(a,b),
解:(1)设A(a,b),
∵OA与x轴所成的角为45°,
∴a=b,
∵点A在y1=$\frac{12}{x}$(x>0)图象上,
∴ab=12,
∵a=b=2$\sqrt{3}$,
∴A点的坐标为(2$\sqrt{3}$,2$\sqrt{3}$);
(2)如图1,过A、B分别作y轴的垂线,垂足为C、D,
∵∠AOB=90°,
∴∠COB+∠AOD=90°,
∵∠CBO+∠COB=90°,
∴∠CBO=∠AOD,
∵∠BCO=∠ADO=90°,
∴△AOC∽△OBD,
∴$\frac{OA}{OB}$=$\sqrt{\frac{{S}_{△AOC}}{{S}_{△OBD}}}$=$\sqrt{\frac{\frac{1}{2}×12}{\frac{1}{2}×3}}$=2;
(3)∵点B的横坐标为-2,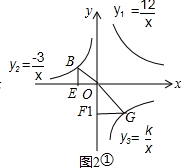
∴B(-2,$\frac{3}{2}$),
∵函数y3=$\frac{k}{x}$(x<0)的图象与y1=$\frac{12}{x}$(x>0)的图象关于x轴对称,
∴y3=$\frac{-12}{x}$,(x>0),
设G(a,-$\frac{12}{a}$),
①当∠OFG=90°,∠OGF=∠OBE时,如图2①,
∴△OBE∽△GOF,
∴$\frac{a}{\frac{3}{2}}$=$\frac{\frac{12}{a}}{2}$,解a=3,
∴-$\frac{12}{a}$=-4,
∴F(0,-4);
②当∠OFG=90°,∠OFG=∠OBE时,如图2①,
∴△OBE∽△GOF,
∴$\frac{\frac{12}{a}}{\frac{3}{2}}$=$\frac{a}{2}$,解得a=4,
∴-$\frac{12}{a}$=-3,
∴F(0,-3);
③当∠OGF=90°,∠GOF=∠OBE时, 如图2②,
如图2②,
∴△OBE∽△OGH,
∴$\frac{\frac{12}{a}}{2}$=$\frac{a}{\frac{3}{2}}$,
∴a=3,
∴G(3,-4)
∵GH2=OH•FH,
∴FH=$\frac{9}{4}$,
∴OF=4+$\frac{9}{4}$=$\frac{25}{4}$,
∴F(0,-$\frac{25}{4}$);
④当∠OGF=90°,∠FOG=∠OBE时,如图2②
∴△OBE∽△GHO,
∴$\frac{\frac{12}{a}}{\frac{3}{2}}$=$\frac{a}{2}$,解得a=4,
∴G(4,-3)
∵GH2=OH•FH,
∴FH=$\frac{16}{3}$,
∴OF=3+$\frac{16}{3}$=$\frac{25}{3}$,
∴F(0,-$\frac{25}{3}$);
点评 本题考查了反比例函数图象上点的坐标特征,三角形相似的判定和性质,等腰直角三角形的性质等,分类讨论思想的运用是解题的关键.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 正方形网格中,△ABC如图放置,则sin∠BAC=( )
正方形网格中,△ABC如图放置,则sin∠BAC=( )| A. | $\frac{2}{{\sqrt{13}}}$ | B. | $\frac{3}{{\sqrt{13}}}$ | C. | $\frac{4}{{\sqrt{13}}}$ | D. | $\frac{12}{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
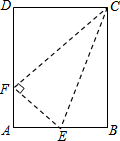 如图,已知矩形ABCD的两边AB与BC的比为4:5,E是AB上的一点,沿CE将△EBC向上翻折,若B点恰好落在边AD上的F点,则tan∠DCF=$\frac{3}{4}$.
如图,已知矩形ABCD的两边AB与BC的比为4:5,E是AB上的一点,沿CE将△EBC向上翻折,若B点恰好落在边AD上的F点,则tan∠DCF=$\frac{3}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com