
����Ŀ����ͼ������ABC�У�AB=AC����ABC�͡�ACB��ƽ���߽��ڵ�O.
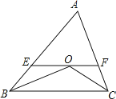
(1) ���ͼ�Σ�����д������Ϊ��ȷ�Ľ��ۣ�
(2) ��O��EF��BC��AB��E����AC��F. ����д��ͼ�����е��������Σ���̽��EF��BE��FC֮��Ĺ�ϵ��

(3) ��AB��AC�������������䣬ͼ�л��е��������������У���д�����еĵ��������Σ���û�У���˵�����ɣ��߶�EF��BE��FC֮�䣬����̽���Ľ����Ƿ�����
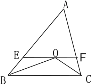
���𰸡���1�����ۣ���ABO=��CBO=��ACO=��BCO��������۲�Ψһ����ȷ���ɣ������������������2�������������У���ABC����AEF����BEO����COF����BOC��EF��BE��FC֮��Ĺ�ϵEF=BE+CF�� ���������������3��ͼ�еĵ����������У���BEO����COF ��������Ȼ�����������������.
��������
��1�������ۣ���ABO=��CBO=��ACO=��BCO�����ݵ��������ε����ʼ���ƽ���ߵĶ��弴��֤��������𰸲�Ψһ������2�������������У���ABC����AEF����BEO����COF����BOC��EF��BE��FC֮��Ĺ�ϵEF=BE+CF���ɣ�1���ɵã���ABC����BOC�ǵ��������Σ���ƽ���ߵ����ʼ����������ε��������ж�����֤�á�AEF�ǵ��������Σ���ƽ���ߵ����ʼ���ƽ���ߵĶ��弴��֤�á�BEO����COF�ǵ��������Σ�EF=BE+CF����2��ͼ�еĵ����������У���BEO����COF ��������Ȼ��������ȣ�2���ķ���֤������.
��1�����ۣ���ABO=��CBO=��ACO=��BCO���������£�
��AB=AC�����ABC=��ACB��
��OBƽ�֡�ABC��OCƽ�֡�ACB��
���ABO=��CBO=��ACO=��BCO��
��2�������������У���ABC����AEF����BEO����COF����BOC��EF��BE��FC֮��Ĺ�ϵEF=BE+CF�� �������£�
�ɣ�1���ɵã���ABC����BOC�ǵ��������Σ�
��EF��BC��
���ABC=��AEF����AFE=��ACB,
�ߡ�ABC=��ACB��
���AEF=��AFE��
��AE=AF,
����AEF�ǵ��������Σ�
��BOƽ�֡�ABC��
���EBO=��OBC��
��EF��BC��
���OBC=��EOB��
���EBO=��EOB��
��EO=BE��
���BEO�ǵ��������Σ�
ͬ���ɵ�OF=FC��
���COF�ǵ��������Σ�
��EO+OF=BE+FC��
��EF=BE+CF��
��3��ͼ�еĵ����������У���BEO����COF ��������Ȼ�������������£�
��BOƽ�֡�ABC��
���EBO=��OBC��
��EF��BC��
���OBC=��EOB��
���EBO=��EOB��
��EO=BE��
���BEO�ǵ��������Σ�
ͬ���ɵ�OF=FC��
���COF�ǵ��������Σ�
��EO+OF=BE+FC��
��EF=BE+CF��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����20�����ӣ���ÿ��20ǧ��Ϊ������������IJ��ֱַ���������������ʾ����¼���£�
��������IJ�(��λ��ǧ��) | ��2 | ��1.5 | ��1 | 0 | 1 | 1.5 |
�� �� | 1 | 4 | 2 | 3 | 2 | 8 |
(1)�����ص�һ��������һ���ض��٣�
(2)��20�����ӵ��������Ƕ���ǧ�ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ƽ��ֱ������ϵ�У��߳�Ϊ8��������OABC���������������ϣ���ͼ����

��1�����A��B��C�����꣮
��2������A��C�����ֱ��l����һ��P����D��0��6����y���������ϣ���PD��PB����ͼ1������PB2��PD2��24�����ı���PBCD�������
��3������E��0��1������N��2��0������ͼ2����������2�����еĵ�P��һ��ƽ����y���ֱ��m����ֱ��m���Ƿ����һ��M��ʹ����MNEΪֱ�������Σ������ڣ���M������ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�ۿ�Pλ���ϱ�����ĺ������ϣ������Ǵ�.��Զ�����š����������������ִ�ͬʱ�뿪�ۿ�P�������ع̶������У���Զ������ÿСʱ����12n mile������������ÿСʱ����16n mile�������뿪�۶���1Сʱ�ֱ�A��B����λ�ã���AB=20n mile����֪��Զ���������ű�ƫ��60�������У���ô���������ź��еķ�����________.
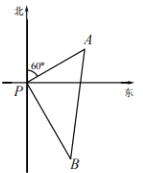
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У�![]() ��
��![]() ��ƽ���߽�BC��O����OBΪ�뾶����O.��1���ж�ֱ��AC�Ƿ��ǡ�O�����ߣ���˵������;
��ƽ���߽�BC��O����OBΪ�뾶����O.��1���ж�ֱ��AC�Ƿ��ǡ�O�����ߣ���˵������;
��2������AO����O�ڵ�E�����ӳ��߽���O�ڵ�D��![]() ����
����![]() ��ֵ;
��ֵ;
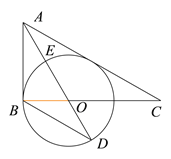
��3���ڣ�2���������£���![]() �İ뾶Ϊ3����AC�ij�.
�İ뾶Ϊ3����AC�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�������ݳ�����ͨѹ���������ϲ�����ͨ������4.18�������裮ij���̶ӳе���ij��·900�׳��ĸ��������̶��ڸ�����360��·�����������豸��ÿ��Ĺ���Ч�ʱ�ԭ�������20%���������27��������������������豸ǰ���̶�ÿ������·�����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������![]() ��
��![]() ������A��ʾ����Ϊ-2��
������A��ʾ����Ϊ-2��![]() ��ʾ����Ϊ2�����������ϴ���һ��
��ʾ����Ϊ2�����������ϴ���һ��![]() ��ʹ��
��ʹ��![]() ����Ƶ�
����Ƶ�![]() ������
������![]() ��
��![]() ����
����![]() �ڵ���������ͼ1��ʾ������
�ڵ���������ͼ1��ʾ������![]() ��ʾ����Ϊ0����
��ʾ����Ϊ0����![]() ����Ƶ�
����Ƶ�![]() Ϊ��
��![]() ��
��![]() ����4�ڵ���.
����4�ڵ���.

����������涨�ش��������⣺
��1������![]() ��
��![]() ��
��![]() ����
����![]() �ڵ������ҵ�
�ڵ������ҵ�![]() �������ϱ�ʾ����Ϊ-4����
�������ϱ�ʾ����Ϊ-4����![]() ��ֵ.
��ֵ.
��2������![]() �������ϵ�
�������ϵ�![]() ��
��![]() ����5�ڵ���������ֱ��д����
����5�ڵ���������ֱ��д����![]() ��ʾ����Ϊ____________��
��ʾ����Ϊ____________��
��3������![]() �������ϣ�����
�������ϣ�����![]() ��
��![]() �غϣ�������
�غϣ�������![]() ��
��![]() ֮��ľ�����
֮��ľ�����![]() ��
��![]() ֮������һ�룬�Ҵ�ʱ��
֮������һ�룬�Ҵ�ʱ��![]() Ϊ��
��![]() ��
��![]() ����
����![]() �ڵ�������
�ڵ�������![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC�У���BAC=90������O����ABC����ƽ����һ�㣬����OA���ӳ�OA����E��ʹ��AE=OA������OC������B��BD��OCƽ�У���ʹ��DBC=��OCB����BD=OC������DE.
(1)��ͼһ������O��Rt��ABC�ڲ�ʱ.

�ٰ����ⲹȫͼ�Σ�
�ڲ���DE��BC��������ϵ����֤��.
(2)��AB=AC(��ͼ��)���ҡ�OCB=30������OBC=15�������AED�Ĵ�С.


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ����У���ƻ������Ϊ1800m2����������̻������żס����������̶����.��֪��ÿ��������̻���������Ҷ�ÿ��������̻��������2���������ڶ���������Ϊ400 m2������̻�ʱ���ӱ��Ҷ�����4��.
��1����ס��������̶�ÿ��������̻�������ֱ��Ƕ���m2��
��2����ѧУÿ���踶���ӵ��̻�������0.4��Ԫ���Ҷ�Ϊ0.25��Ԫ��Ҫʹ��ε��̻��ܷ��ò�����8��Ԫ������Ӧ���żӹ��������죿
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com