
【题目】平面直角坐标系![]() 中,
中,![]() ,
,![]() 分别在
分别在![]() 轴正半轴和
轴正半轴和![]() 轴负半轴上,
轴负半轴上,![]() 在第二象限,满足:
在第二象限,满足:![]() ,
,![]() .已知
.已知![]() .
.
(1)求![]() ,
,![]() 的坐标;
的坐标;
(2)求点![]() 的坐标及
的坐标及![]() 的面积;
的面积;
(3)已知![]() 是
是![]() 轴的正半轴上一点,
轴的正半轴上一点,![]() ,
,![]() 在第一象限,
在第一象限,![]() ,
,![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() .
.
①求证:![]() .
.
②在点![]() 的移动过程中,给出以下两个结论:(i)
的移动过程中,给出以下两个结论:(i)![]() 的值不变;(ii)
的值不变;(ii)![]() 的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
【答案】(1)A(0,4),B(-2,0);
(2)C(-4,6);10.
(3)①见详解;②![]() 的值不变,等于
的值不变,等于![]() .
.
【解析】
(1)根据非负数的性质,即可求出结果;
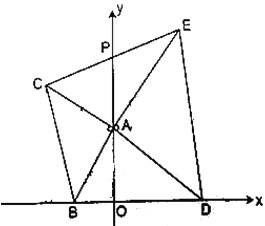
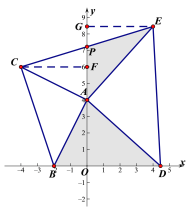
(2)如图,过点C作CF⊥y轴于F,先证△ACF≌△BAO,从而得到CF=OA,AF=OB,又因为点C在第四象限,故可得点C的坐标,根据勾股定理求得AC=AB=2![]() ,再根三角形的面积计算公式即可求得△ABC的面积;
,再根三角形的面积计算公式即可求得△ABC的面积;
(3)①过点E作EG⊥y轴于点G,先证△AGE≌△DOA,得到GE=OA=4,故GE=CF,再根据AAS证得△GPE≌△FOC,从而得到PC=PE;②利用面积法进行等量代换即可得到![]() =
=![]() .
.
解:(1)∵![]() ,
,
∴![]() ,解得:
,解得:![]() .
.
∴A(0,4),B(-2,0).
(2)过点C作CF⊥y轴于F,
∴∠CFA=∠AOB=90°,
∴∠CAF+∠ACF=90°.
∵![]() ,
,
∴∠CAF+∠BAO=90°.
∴∠ACF=∠BAO
在△ACF和△BAO中
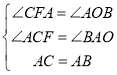
∴△ACF≌△BAO.
∴CF=OA=4,AF=OB=2
∵点C在第二象限,
∴C(-4,6).
在Rt△ABO中,
AB=![]() =
=![]() =2
=2![]() .
.
∵∠BAC=90°,AC=AB=2![]() .
.
∴![]() =
=![]() AC=
AC=![]() =10.
=10.
(3)①过点E作EG⊥y轴于G,
∵∠EAD=90°,
∴∠DAO+∠GAE=90°.
∵∠AEG+∠GAE=90°,
∴∠DAO=∠AEG.
在△AOD和△EGA中
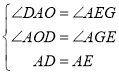
∴△AOD≌△EGA.
∴GE=OA=4.
∵CF=OA,
∴CF=GE.
∵CF⊥y轴,EG⊥y轴,
∴∠PGE=∠PFC=90°.
在△FPC和△GPE中
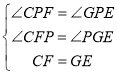
∴△FPC≌△GPE.
∴PC=PE.
②![]() 的值不变,理由如下:
的值不变,理由如下:
∵PC=PE,
∴![]() =
=![]() =
=![]() .
.
∴![]() =
=![]()
∵△ACF≌△BAO,
∴![]() =
=![]() .
.
∵△AOD≌△EGA.
∴![]() =
=![]()
∵![]() =
=![]() +
+![]()
∴![]() =
=![]() +
+![]()
∵![]() =
=![]() +
+![]()
∴![]() =
=![]() +
+![]() +
+![]()
=![]() +
+![]() +
+![]()
=![]() .
.
∴![]() =
=![]() =
=![]() .
.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD的边长为2,∠B=60°,点P、Q分别是边BC、CD上的动点(不与端点重合),且BP=CQ.

(1)图中除了△ABC与△ADC外,还有哪些三角形全等,请写出来;
(2)点P、Q在运动过程中,四边形APCQ的面积是否变化,如果变化,请说明理由;如果不变,请求出面积;
(3)当点P在什么位置时,△PCQ的面积最大,并请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是ts(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(1)求证:四边形AEFD是平行四边形;
(2)当t为何值时,△DEF为直角三角形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则下列结论:①4ac﹣b2<0;②2a﹣b=0;③a+b+c<0;④点M(x1,y1)、N(x2,y2)在抛物线上,若x1<x2,则y1≤y2,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=BC=2CD,AB∥CD,∠C=90°,E是BC的中点,AE与BD相交于点F,连接DE.

(1)求证:△ABE≌△BCD;
(2)判断线段AE与BD的数量关系及位置关系,并说明理由;
(3)若CD=1,试求△AED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强学生课外阅读,开阔视野,某校开展了“书香校园,从我做起”的主题活动,学校随机抽取了部分学生,对他们一周的课外阅读时间进行调查,绘制出频率分布表和频率直方图的一部分如下:
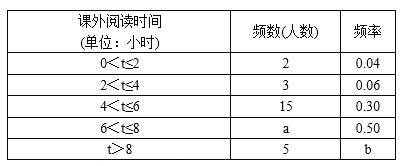
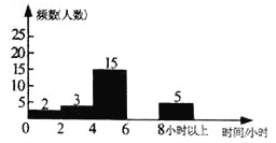
请根据图表信息回答下列问题:
(1)频数分布表中的a=____________,b=____________;
(2)将频数直方图补充完整;
(3)学校将每周课外阅读时间在6小时以上的学生评为“阅读之星”,请你估计该校2 000名学生中评为“阅读之星”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )

A. 两车到第3秒时行驶的路程相等B. 在4至8秒内甲的速度都大于乙的速度
C. 乙前4秒行驶的路程为48米D. 在0到8秒内甲的速度每秒增加4米/秒
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果以13元/千克的价格销售,那么每天可售出240千克.
小红:通过调查验证,我发现每天的销售量y(千克)与销售单价x(元)之间存在一次函数关系,每天销售200千克以上.
(1)求每天的销售量y(千克)与销售单价x(元)之间的函数关系式;
(2)该超市销售这种水果每天获取的利润达到1040元,那么销售单价为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com