
 已知一次函数y=kx+b的图象经过点A(2,0),与y轴交于点B(0,4).
已知一次函数y=kx+b的图象经过点A(2,0),与y轴交于点B(0,4).分析 (1)把点A(2,0),点B(0,4)代入y=kx+b中,得出k,b的值,从而得出一次函数的表达式,再画出图象即可;
(2)把x=-5代入一次函数的表达式即可得出y的值;
(3)根据图象直接得出y的取值范围即可.
解答 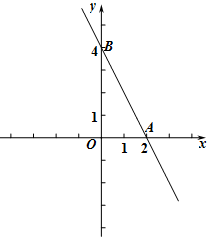 解:(1)将A(2,0),B(0,4)代入y=kx+b中
解:(1)将A(2,0),B(0,4)代入y=kx+b中
得,$\left\{\begin{array}{l}2k+b=0\\ b=4\end{array}\right.$
解得,$\left\{\begin{array}{l}k=-2\\ b=4\end{array}\right.$
∴y=-2x+4;
其图象如右图所示;
(2)当x=-5时,y=-2×(-5)+4=14;
(3)y<4.
点评 本题考查了用待定系数法求一次函数的解析式,以及一次函数的图象和图象上点的坐标特征,掌握用待定系数法求一次函数的解析式是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
| 抛掷次数n | 100 | 200 | 300 | 400 | 600 | 800 | 1000 |
| 针尖不着地的频数m | 64 | 118 | 189 | 252 | 360 | 488 | 610 |
| 针尖不着地的频数$\frac{m}{n}$ | 0.64 | 0.59 | 0.63 | 0.63 | 0.60 | 0.61 | 0.61 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a-3<b-3 | B. | -2a<-2b | C. | 0.7a<0.7b | D. | -$\frac{a}{4}$$>-\frac{b}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
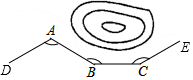 如图所示,一条公路修到湖边时,需要拐弯绕湖而过,第一次拐的角∠A=120°,第二次拐的角∠B=165°,则第三次拐的角∠C=135°时道路CE才能恰好与AD平行.
如图所示,一条公路修到湖边时,需要拐弯绕湖而过,第一次拐的角∠A=120°,第二次拐的角∠B=165°,则第三次拐的角∠C=135°时道路CE才能恰好与AD平行.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月用水量/t | 单价/(元/t) |
| 不大于10t部分 | 1.5 |
| 大于10t且不大于mt部分20≤m≤50 | 2 |
| 大于mt部分 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲、乙两车分别从M、N两地相向而行,甲车出发1小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图是甲乙两车之间的距离s(千米)与甲车出发时间t(小时)之间的函数图象,其中D点表示甲车到达N地,停止行驶.
甲、乙两车分别从M、N两地相向而行,甲车出发1小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图是甲乙两车之间的距离s(千米)与甲车出发时间t(小时)之间的函数图象,其中D点表示甲车到达N地,停止行驶.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com