
【题目】如图,B是线段AD上一动点,沿A→D→A以2cm/s的速度往返运动1次,C是线段BD的中点,AD=10cm,设点B运动时间为t秒(0≤t≤10).
![]()
(1)当t=2时,①AB= ___ cm.②求线段CD的长度.
(2)用含t的代数式表示运动过程中AB的长.
(3)在运动过程中,若AB中点为E,则EC的长是否变化?若不变,求出EC的长;若发生变化,请说明理由.
【答案】(1)①4;②3;(2)①当![]() 时,
时, ![]() ,②当
,②当![]() 时,
时, ![]() ;(3)在运动过程中EC的长保持不变,恒等于5.
;(3)在运动过程中EC的长保持不变,恒等于5.
【解析】试题分析:(1)①根据AB=2t即可得出结论;
②先求出BD的长,再根据C是线段BD的中点即可得出CD的长;
(2)根据AB=2t即可得出结论;
(3)直接根据中点公式即可得出结论.
试题解析:(1)当t=2时,①AB= 4 cm.
②解:∵![]()
又∵![]() ,
, ![]()
∴![]()
∵点C是线段BD的中点
∴![]()
(2)①当![]() 时,此时点B从A向D移动:
时,此时点B从A向D移动: ![]()
②当![]() 时,此时点B从D向A移动:
时,此时点B从D向A移动: ![]()
(3)①当![]() 时,此时点B从A向D移动:
时,此时点B从A向D移动:
∵点E是AB的中点, ![]()
∴![]()
∵![]() ,
, ![]()
∴![]()
∵点C是BD的中点
∴![]()
又∵![]()
∴![]()
②当![]() 时,此时点B从D向A移动:
时,此时点B从D向A移动:
∵点E是AB的中点, ![]()
∴![]()
∵![]() ,
, ![]()
∴![]()
∵点C是BD的中点
∴![]()
又∵![]()
∴![]()
综上所述:在运动过程中EC的长保持不变,恒等于5.


科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BC,垂足为点E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF,EG,AG,∠1=∠2.
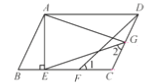
(1)若CF=2,AE=3,求BE的长;
(2)求证:∠CEG=![]() ∠AGE.
∠AGE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,点P是CD的中点,∠BCD=60°,射线AP交BC的延长线于点E,射线BP交DE于点K,点O是线段BK的中点,作BM⊥AE于点M,作KN⊥AE于点N,连结MO、NO,以下四个结论:①△OMN是等腰三角形;②tan∠OMN= ![]() ;③BP=4PK;④PMPA=3PD2 , 其中正确的是( )
;③BP=4PK;④PMPA=3PD2 , 其中正确的是( )
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育委员统计了全班学生“1分钟跳绳”的次数,绘制成如下两幅统计图:

根据这两幅统计图的信息完成下列问题
(1)这个班共有学生多少人?并补全频数分布直方图;
(2)如果将“1分钟跳绳”的次数大于或等于180个定为优秀,请你求出这个班“1分钟跳绳”的次数达到优秀的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=∠COD=90°,OE平分∠BOD,若∠AOD∶∠BOC=5∶1,则∠COE的度数为( )

A. 30° B. 40° C. 50° D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生的身体素质,某校规定学生每天参加户外活动的平均时间不少于1小时,为了解学生参加户外活动的情况,对该校七年级部分学生参加户外活动的时间进行调查,并将调查结果绘制成如下两幅不完整的统计图,请根据图中提供的信息解答下列问题:

(1)填空:这次调查的学生共 人,表示户外活动时间为1小时的扇形圆心角度数是 度;
(2)求参加户外活动的时间为1.5小时的学生人数,并补全频数分布直方图;
(3)若该校七年级有学生600人,请估计该校七年级学生参加户外活动的时间不少于1小时的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知点E,F,G,H分别是四边形ABCD各边AB,BC,CD,DA的中点,根据以下思路可以证明四边形EFGH是平行四边形:
(1)如图2,将图1中的点C移动至与点E重合的位置,F,G,H仍是BC,CD,DA的中点,求证:四边形CFGH是平行四边形;
(2)如图3,在边长为1的小正方形组成的5×5网格中,点A,C,B都在格点上,在格点上画出点D,使点C与BC,CD,DA的中点F,G,H组成正方形CFGH;
(3)在(2)条件下求出正方形CFGH的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以AB为直径的⊙O经过点P,C是⊙O上一点,连接PC交AB于点E,且∠ACP=60°,PA=PD. 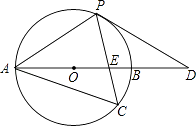
(1)试判断PD与⊙O的位置关系,并说明理由;
(2)若 ![]() :
: ![]() =1:2,求AE:EB:BD的值(请你直接写出结果);
=1:2,求AE:EB:BD的值(请你直接写出结果);
(3)若点C是弧AB的中点,已知AB=4,求CECP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,把矩形沿AC折叠,点B落在点E处,AE与DC的交点为O,连接DE.
(1)求证:△ADE≌△CED;
(2)求证:DE∥AC.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com