
【题目】如图,已知菱形ABCD中,∠BAD=60°,点E、F分别是AB、AD上两个动点,若AE=DF,连接BF与DE相交于点G,连接CG,与BD相交于H。
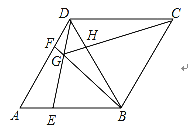
(1)求∠BGE的大小;(2)求证:GC平分∠BGD.
【答案】(1)∠BGE=60°;(2)见解析.
【解析】
(1)由题意可证△ADB是等边三角形,可得AD=AB=BD,∠DAB=∠ADB=∠ABD,由“SAS”可证△ADE≌△DBF,可得∠ADE=∠DBF,由三角形外角性质可求∠BGE的大小;
(2)过点C作CN⊥BF于点N,过点C作CM⊥ED于点M,由“AAS”可证Rt△CBN≌Rt△CDM,可得CM=CN,由角平分线的性质可得结论.
(1)∵ABCD为菱形,
∴AB=AD.
∵∠BAD=60°,
∴△ABD为等边三角形.
∴∠A=∠BDF=60°.
又∵AE=DF,AD=BD,
∴△AED≌△DFB;
∴∠DBG=∠ADE
∴∠EGB=∠DBG+∠BDG=∠ADE+∠BDG=∠ADB=60°
(2)如图,过点C作CN⊥BF于点N,过点C作CM⊥ED于点M,

由(1)得∠ADE=∠DBF
∴∠CBF=60°+∠DBF
=60°+∠ADE
=∠DEB
又∠DEB=∠MDC
∴∠CBF=∠CDM
∵BC=CD,∠CBF=∠CDM,∠CMD=∠CNG=90°
∴Rt△CBN≌Rt△CDM(AAS)
∴CN=CM,且CN⊥BF,CM⊥ED
∴点C在∠BGD的平分线上
即GC平分∠BGD.


科目:初中数学 来源: 题型:
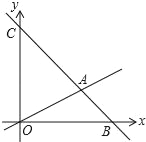
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)是否存在点M,使△OMC的面积是△OAC的面积的![]() ?若存在求出此时点M的坐标;若不存在,说明理由.
?若存在求出此时点M的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N.当∠MAN绕点A旋转到BM=DN时(如图1),易证BM+DN=MN.
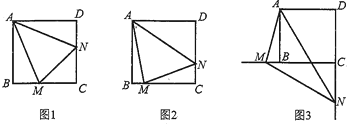
(1)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM、DN和MN之间有怎样的数量关系?写出猜想.并加以证明.
(2)当∠MAN绕点A旋转到如图3位置时,线段BM、DN和MN之间有怎样的数量关系?请写出你的猜想,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个形状,大小完全相同的含有30°,60°的三角板如图①放置,PA,PB与直线MN重合,且三角板PAC与三角板PBD均可绕点P逆时针旋转。
(1)试说明:∠DPC=90°;
(2)如图②,若三角板PAC的边PA从PN处开始绕点P逆时针旋转一定度数,PF平分![]() ,PE平分
,PE平分![]() ,求
,求![]() 。
。
(3)如图③,若三角板PAC的边PA从PN处开始绕点P逆时针旋转,转速为3。/s。同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速为2。/s,在两个三角板旋转过程中(PC转到与PM重合时,三角板都停止转运),问![]() 的值是否变化?若不变,求出其值,若变化,说明理由。
的值是否变化?若不变,求出其值,若变化,说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校课外小组为了解同学们对学校“阳光跑操”活动的喜欢程度,抽取部分学生进行调查.被调查的每个学生按A(非常喜欢)、B(比较喜欢)、C(一般)、D(不喜欢)四个等级对活动评价.图1和图2是该小组采集数据后绘制的两幅统计图.经确认扇形统计图是正确的,而条形统计图尚有一处错误且并不完整.请你根据统计图提供的信息,解答下列问题:

(1)此次调查的学生人数为___;
(2)条形统计图中存在错误的是___(填A. B.C中的一个),并在图中加以改正;
(3)在图2中补画条形统计图中不完整的部分;
(4)如果该校有600名学生,那么对此活动“非常喜欢”和“比较喜欢”的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
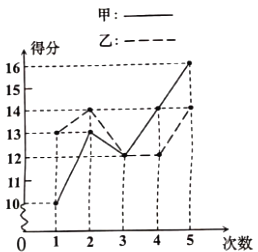
【题目】甲乙两人参加某项体育训练,近期五次测试成绩得分情况如图所示:
(1)分别求出两人得分的平均数;
(2)谁的方差较大?
(3)根据图表和(1)的计算,请你对甲、乙两人的训练成绩作出评价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,王老师布置如下任务:
如图1,△ABC中,BC>AB>AC,在BC边上取一点P,使∠APC=2∠ABC.
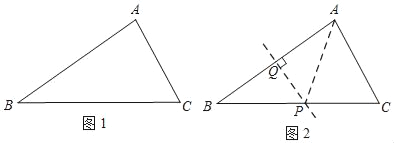
小路的作法如下,如图2:
①作AB边的垂直平分线,交BC于点P;
②连结AP.
所以,∠APC=2∠ABC.
小路的作图依据是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解七年级学生的身体素质情况,体育老师对该年级部分学生进行了一分钟跳绳次数的测试,并把测试成绩绘制成如图所示的频数表和频数直方图(每组含前一个边界值,不含后一个边界值).


(1)参加测试的学生有多少人?
(2)求![]() ,
,![]() 的值,并把频数直方图补充完整.
的值,并把频数直方图补充完整.
(3)若该年级共有![]() 名学生,估计该年级学生一分钟跳绳次数不少于
名学生,估计该年级学生一分钟跳绳次数不少于![]() 次的人数.
次的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com