
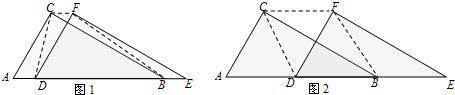
| AB2-AC2 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |


 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
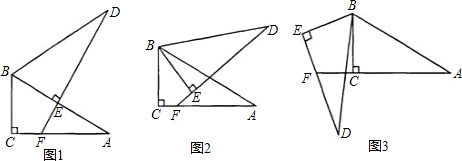
查看答案和解析>>
科目:初中数学 来源: 题型:
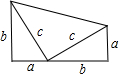 曾任美国总统的加菲尔德在《新英格兰教育日志》上发表了他提出的一个勾股定理的证明.如图,这就是他用两个全等的直角三角形拼出的图形.上面的图形整体上拼成一个直角梯形.所以它的面积有两种表示方法.既可以表示为
曾任美国总统的加菲尔德在《新英格兰教育日志》上发表了他提出的一个勾股定理的证明.如图,这就是他用两个全等的直角三角形拼出的图形.上面的图形整体上拼成一个直角梯形.所以它的面积有两种表示方法.既可以表示为查看答案和解析>>
科目:初中数学 来源: 题型:
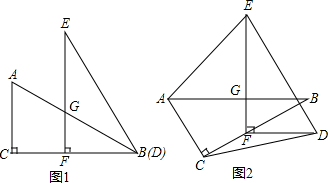
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com