
【题目】在矩形![]() 内放置正方形甲、正方形乙、等腰直角三角形丙,它们的摆放位置如图所示,已知
内放置正方形甲、正方形乙、等腰直角三角形丙,它们的摆放位置如图所示,已知![]() ,图中阴影部分的面积之和为31,则矩形
,图中阴影部分的面积之和为31,则矩形![]() 的周长为___________.
的周长为___________.

【答案】![]()
【解析】
设甲正方形的边长为a,乙正方形的边长为b,结合图形特征及隐含的关系式,用含a,b的代数式表示出有关线段,再利用![]() 建立方程,得到a=
建立方程,得到a=![]() ,再统一用b表示出各个部分的面积,运用阴影部分的面积之和为31建立方程解得b的值,从而求得矩形的周长.
,再统一用b表示出各个部分的面积,运用阴影部分的面积之和为31建立方程解得b的值,从而求得矩形的周长.
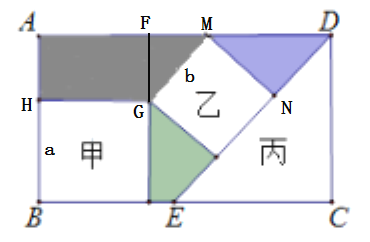
解:设甲正方形的边长为a,乙正方形的边长为b,则HB=HG=AF=a,GM=MN=b,
如图过点G作GF⊥AD,则![]() 为等腰直角三角形
为等腰直角三角形
∴FG=FM=AH=![]() GM=
GM=![]() b,MD=
b,MD=![]() MN=
MN=![]() b,
b,
∴AB=BH+AH=a+![]() b,BC=AD=AF+FM+MD=a+
b,BC=AD=AF+FM+MD=a+![]() b+
b+![]() b=a+
b=a+![]() b,
b,
∵AB:BC=5:9,
∴( a+![]() b) :(a+
b) :(a+![]() b)=5 :9,
b)=5 :9,
解得:a=![]() ,
,
∴CD=AB= a+![]() b=
b=![]() +
+![]() b=
b=![]() ,BC=
,BC=![]()
∴![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
而 ![]()
![]() =
=![]() ,
,
![]() ,
,
∵![]() =31,
=31,
∴![]() =16
=16
∴b=4
∴矩形![]() 的周长为2(AB+BC)=2(
的周长为2(AB+BC)=2(![]() )=
)=![]()
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中①△ABD≌△BCF;②四边形BDEF是平行四边形;③S四边形BDEF=![]() ;④S△AEF=
;④S△AEF=![]() .其中正确的有( )
.其中正确的有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,把矩形OCBA绕点C顺时针旋转α角,得到矩形FCDE,设FC与AB交于点H,且A(0,4),C(6,0).
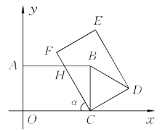
(1)当α=45°时,求H点的坐标.
(2)当α=60°时,ΔCBD是什么特殊的三角形?说明理由.
(3)当AH=HC时,求直线HC的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】AB∥CD,直线a交AB、CD分别于点E、F,点M在EF上,P是直线CD上的一个动点,(点P不与F重合)
(1)当点P在射线FC上移动时,∠FMP+∠FPM =∠AEF成立吗?请说明理由。
(2)当点P在射线FD上移动时,∠FMP+∠FPM与∠AEF有什么关系?并说明你的理由


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个单位为1的方格纸上,△A1A2A3 , △A3A4A5 , △A5A6A7 , …,是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,﹣1),A3(0,0),则依图中所示规律,A2017的横坐标为( )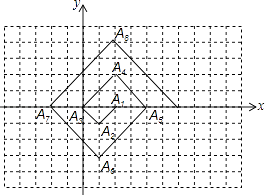
A.1010
B.2
C.1
D.﹣1006
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣2(m+1)x+m2+2=0
(1)若方程有实数根,求实数m的取值范围;
(2)若方程两实数根分别为x1、x2 , 且满足x12+x22=10,求实数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从数﹣2,﹣ ![]() ,0,4中任取一个数记为m,再从余下的三个数中,任取一个数记为n,若k=mn,则正比例函数y=kx的图象经过第三、第一象限的概率是 .
,0,4中任取一个数记为m,再从余下的三个数中,任取一个数记为n,若k=mn,则正比例函数y=kx的图象经过第三、第一象限的概率是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com