
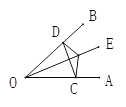
【题目】如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.
求证:(1)∠ECD=∠EDC;
(2)OC=OD;
(3)OE是线段CD的垂直平分线.
【答案】(1)证明见解析(2)证明见解析(3)证明见解析
【解析】试题分析:(1)根据角平分线性质可证ED=EC,从而可知△CDE为等腰三角形,可证∠ECD=∠EDC;
(2)由OE平分∠AOB,EC⊥OA,ED⊥OB,OE=OE,可证△OED≌△OEC,可得OC=OD;
(3)根据ED=EC,OC=OD,可证OE是线段CD的垂直平分线.
试题解析:证明:(1)∵OE平分∠AOB,EC⊥OA,ED⊥OB,∴ED=EC,即△CDE为等腰三角形,∴∠ECD=∠EDC;
(2)∵点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,∴∠DOE=∠COE,∠ODE=∠OCE=90°,OE=OE,∴△OED≌△OEC(AAS),∴OC=OD;
(3)∵OC=OD,且DE=EC,∴OE是线段CD的垂直平分线.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:
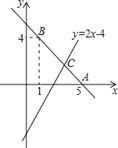
【题目】已知直线y=kx+b经过点A(5,0),B(1,4).
(1)求直线AB的解析式;
(2)若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式2x﹣4>kx+b的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,BA=BC.点D是AB的中点,连接CD,过点B作BG丄CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连接DF.给出以下四个结论:
①![]() ; ②点F是GE的中点; ③AF=
; ②点F是GE的中点; ③AF=![]() AB;④S△ABC=5S△BDF,其中正确的结论序号是__________.
AB;④S△ABC=5S△BDF,其中正确的结论序号是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国是一个严重缺水的国家.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过6吨时,水价为每吨2元,超过6吨时,超过的部分按每吨3元收费.该市某户居民5月份用水x吨,应交水费y元.
(1)若0<x≤6,请写出y与x的函数关系式.
(2)若x>6,请写出y与x的函数关系式.
(3)如果该户居民这个月交水费27元,那么这个月该户用了多少吨水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,直径是50cm圆柱形油槽装入油后,油深CD为15cm,求油面宽度AB的长.

(2)如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,过点C作CF∥BE交DE的延长线于F,连接CD.
①求证:四边形BCFE是菱形;
②在不添加任何辅助线和字母的情况下,请直接写出图中与△BEC面积相等的所有三角形(不包括△BEC).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com