
【题目】如图,在△ABC的一边AB上有一点P.
(1)能否在另外两边AC和BC上各找一点M、N,使得△PMN的周长最短.若能,请画出点M、N的位置,若不能,请说明理由;
(2)若∠ACB=40°,在(1)的条件下,求出∠MPN的度数.

【答案】(1)详见解析.(2)100°.
【解析】
(1)如图:作出点P关于AC、BC的对称点D、G,然后连接DG交AC、BC于两点,标注字母M、N;
(2)根据对称的性质,易求得∠C+∠EPF=180°,由∠ACB=48°,易求得∠D+∠G=48°,即而求得答案.
解:(1)①作出点P关于AC、BC的对称点D、G,
②连接DG交AC、BC于两点,
③标注字母M、N;

(2)∵PD⊥AC,PG⊥BC,
∴∠PEC=∠PFC=90°,
∴∠C+∠EPF=180°,
∵∠C=40°,
∴∠EPF=140°,
∵∠D+∠G+∠EPF=180°,
∴∠D+∠G=40°,
由对称可知:∠G=∠GPN,∠D=∠DPM,
∴∠GPN+∠DPM=40°,
∴∠MPN=140°-40°=100°.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图1,直线y=﹣ ![]() x+n交x轴于点A,交y轴于点C(0,4),抛物线y=
x+n交x轴于点A,交y轴于点C(0,4),抛物线y= ![]() x2+bx+c经过点A,交y轴于点B(0,﹣2).点P为抛物线上一个动点,过点P作x轴的垂线PD,过点B作BD⊥PD于点D,连接PB,设点P的横坐标为m.
x2+bx+c经过点A,交y轴于点B(0,﹣2).点P为抛物线上一个动点,过点P作x轴的垂线PD,过点B作BD⊥PD于点D,连接PB,设点P的横坐标为m. 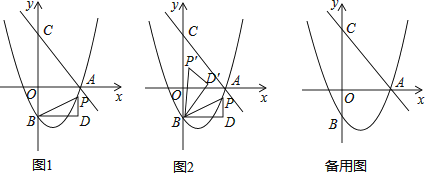
(1)求抛物线的解析式;
(2)当△BDP为等腰直角三角形时,求线段PD的长;
(3)如图2,将△BDP绕点B逆时针旋转,得到△BD′P′,且旋转角∠PBP′=∠OAC,当点P的对应点P′落在坐标轴上时,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,∠AOB . 求作:∠A′O′B′,使∠A′O′B′=∠AOB . 作法:
①以________为圆心,________为半径画弧.分别交OA , OB于点C , D .
②画一条射线O′A′,以________为圆心,________长为半径画弧,交O′A′于点C′,
③以点________为圆心________长为半径画弧,与第2步中所画的弧交于点D′.
④过点________画射线O′B′,则∠A′O′B′=∠AOB .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置,点C1、C2、C3…在x轴上,点A1、A2、A3…在直线l上,A1(0,1),∠A2 A1B1=45°,则点Bn的坐标为____________(用n的代数式表示,n为正整数);

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:
组号 | 分组 | 频数 |
一 | 6≤m<7 | 2 |
二 | 7≤m<8 | 7 |
三 | 8≤m<9 | a |
四 | 9≤m≤10 | 2 |

(1)求a的值;
(2)若用扇形图来描述,求分数在8≤m<9内所对应的扇形图的圆心角大小;
(3)将在第一组内的两名选手记为:A1、A2 , 在第四组内的两名选手记为:B1、B2 , 从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率(用树状图或列表法列出所有可能结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=3,BC=5,以点B为圆心,以任意长为半径作弧,分别交BA、BC于点P、Q,再分别以P、Q为圆心,以大于 ![]() PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为
PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为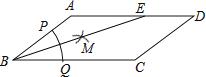
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣2x+m﹣1=0有两个实数根x1 , x2 .
(1)求m的取值范围;
(2)当x12+x22=6x1x2时,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com