
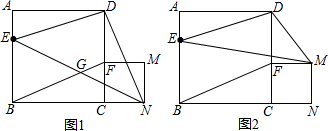
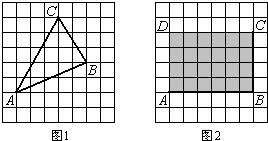
���� ��1����ͼ1����������Ա߷ֱ�ƽ�е��ı�����ƽ���ı��Σ�֤���ı���BEDFΪƽ���ı��Σ�
��2������ͼ1����֤����BCF�ա�DCN����BF=DN����?BEDF����DE=BF����ED=DN����֤��Rt��ADE��Rt��CDN�����ԡ�ADE=��CDN�����EDN�ǵ���ֱ�������Σ�
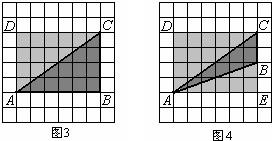
����ͼ2���������ߣ���ʾ��PG��BP��CF�ij�������ƽ��֤����BPG�ס�BCF����ʽ��ʽ�ã�x=2$��\sqrt{2}$��������0��x��1���ó�����ֵ��
��3����ͼ3���������ߣ���������������������ھ��������ȥ����С�����������һ����������õ�����x�Ķ��κ�������ʽ������ֵ���ɣ�
��� 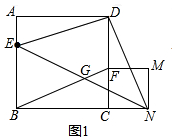 ֤������1����ͼ1�����ı���ABCDΪ�����Σ�
֤������1����ͼ1�����ı���ABCDΪ�����Σ�
��AB��CD��
��DE��BF��
���ı���BEDFΪƽ���ı��Σ�
��2������ͼ1����EDN�ǵ���ֱ�������Σ������ǣ�
���ı���CFMNΪ�����Σ�
��CF=CN����DCN=��DCB=90�㣬
���ı���ABCDΪ�����Σ�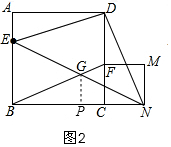
��BC=CD��
���BCF�ա�DCN��
��BF=DN��
���ı���BEDFΪƽ���ı��Σ�
��BF=ED��
��ED=DN��
��AD=DC��
��Rt��ADE��Rt��CDN��
���ADE=��CDN��
�ߡ�ADE+��EDC=90�㣬
���CDN+��EDC=90�㣬
����EDN=90�㣬
���EDN�ǵ���ֱ�������Σ�
�ڹ�G��GP��BN��P����ͼ2����PG��BE��
��BE=x��AE=1-x��
�ɢٵã�CN=AE=1-x��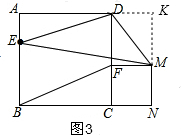
��BN=BC+CN=1+1-x=2-x��
��G��EN���е㣬
��BP=$\frac{1}{2}$BN=$\frac{1}{2}$��2-x��=1-$\frac{x}{2}$��
��PG=$\frac{1}{2}$EB=$\frac{x}{2}$��
��PG��BC��DC��BC��
��PG��DC��
���BPG�ס�BCF��
��$\frac{BP}{BC}=\frac{PG}{CF}$��
��$\frac{1-\frac{x}{2}}{1}$=$\frac{\frac{x}{2}}{1-x}$��
��ã�x=2��$\sqrt{2}$��
��0��x��1����2+$\sqrt{2}$��1��0��2-$\sqrt{2}$��1��
��x=2-$\sqrt{2}$��
��3���ӳ�AD��NM��K��
��S��EDM=S����ABNK-S��ADE-S��DKM-S����EBNM��
=��2-x��•1-$\frac{1}{2}$��1-x��•1-$\frac{1}{2}$•x•��1-x��-$\frac{1}{2}$��1-x+x����2-x����
=$\frac{1}{2}{x}^{2}$-$\frac{1}{2}$x+$\frac{1}{2}$��
=$\frac{1}{2}$��x-$\frac{1}{2}$��2+$\frac{3}{8}$��
��$\frac{1}{2}$��0��
���EDM�����ȡ����Сֵ��
�൱x=$\frac{1}{2}$ʱ����EDM�������Сֵ��$\frac{3}{8}$��
���� �������ı��ε��ۺ��⣬�����������Ρ�ƽ���ı��ε����ʼ�����ֱ�������ε��������ж���֪��������ȵ�ֱ���������ǵ���ֱ�������Σ������Ϊ45�㣬���������ֵ���⣬ת��Ϊ���κ�������ֵ���⣬���������ʽ�ж��κ����ı���ʽ�������䷽����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
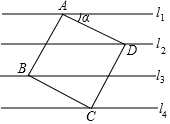 ��ͼ����ֱ֪��l1��l2��l3��l4����������ƽ��ֱ��ľ��붼��1�����������ABCD���ĸ�����ֱ�������ֱ���ϣ���sin��=��������
��ͼ����ֱ֪��l1��l2��l3��l4����������ƽ��ֱ��ľ��붼��1�����������ABCD���ĸ�����ֱ�������ֱ���ϣ���sin��=��������| A�� | $\frac{1}{2}$ | B�� | $\frac{\sqrt{5}}{5}$ | C�� | $\frac{2\sqrt{5}}{5}$ | D�� | $\frac{\sqrt{3}}{2}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com