练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．如图，木杆EF长2m，它的影长FD为3m，测得影长FD为201m，测得OA为201m，求金字塔的高度BO．

    分析 利用“在同一时刻物高与影长的比相等”得到$\frac{BO}{201}$=$\frac{2}{3}$，然后利用比例性质求出OB即可．

    解答 解：根据题意得$\frac{BO}{OA}$=$\frac{EF}{FD}$，即$\frac{BO}{201}$=$\frac{2}{3}$，
    解得BO=134（m）．
    答：金字塔的高度BO为134m．

    点评 本题考查了相似三角形的应用：通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    7．已知抛物线y=-$\frac{1}{4}$x2+bx+c与x轴交于A、B，与y轴交于点C，连结AC、BC，D是线段OB上一动点，以CD为一边向右侧作正方形CDEF，连结BF．若C（0，4），B（4，0）且AO=BO．
    （1）求抛物线的解析式；
    （2）求证：BF⊥AB；
    （3）求∠FBE；
    （4）当D点沿x轴正方向移动到点B时，点E也随着运动，则点E所走过的路线长是4$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

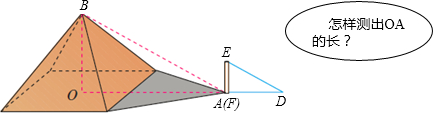
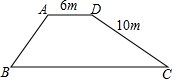    8．如图是一座堤坝的横断面，AB坡坡角为45°，DC坡坡度为1：2，其他数据如图所示，求BC的长（精确到0.1m）．（参考数据：$\sqrt{2}$≈1.414，$\sqrt{5}$≈2.236）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

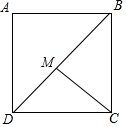    5．如图，在正方形ABCD中，M是对角线BD上一点，若AB=$\sqrt{2}$，则MD+2MC的最小值是$\sqrt{3}$+1，此时∠BMC=60度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

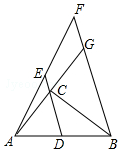    6．如图，△ABC中，∠C=90°，AC=6，BC=8，点D是AB的中点，点E在DC的延长线上，过点B作BF∥DE交AE的延长线于点F，交AC的延长线于点G．
    （1）求证：AC=CG；
    （2）若点P是直线BG上的一点，试确定点P的位置，使△BCP与△BCD相似．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．某服装原价200元，降价x%后再优惠20元，现售价为y元，y关于x的函数关系式是y=-2x+180．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．某市某公交车从起点到终点共有六个站，一辆公交车由起点开往终点，在起点站始发时上了部分乘客，从第二站开始下车、上车的乘客数如表：
    站次
    人数    		二三四五六
    下车（人）3610719
    上车（人）1210940
    （1）求本趟公交车在起点站上车的人数；
    （2）若公交车的收费标准是上车每人2元，计算此趟公交车从起点到终点的总收入？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．某股民在上周星期五买进某种股票，每股80元．如表是本周每日该股票的涨跌情况（单位：元）：
    星期一二三四五
    每股涨跌+6-4.5+5-3.5-7
    星期五收盘时每股64元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图，平行四边形ABCD中，E是CD的延长线上一点，BE与AD交于点F，DE=$\frac{1}{2}$CD．求证：△ABF∽△CEB．

    查看答案和解析>>

    同步练习册答案