
【题目】在等边三角形![]() 中,点
中,点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发沿线段
出发沿线段![]() 的延长线运动,
的延长线运动,![]() 、
、![]() 两点运动的速度相同,
两点运动的速度相同,![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.

(1)如图①,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,求证:
,求证:![]() .
.
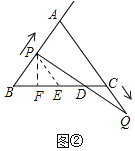
(2)如图②,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() .
.
①当点![]() 在线段
在线段![]() 上运动时,求证:
上运动时,求证:![]() .
.
②当点![]() 在线段
在线段![]() 延长线上运动时,直接写出
延长线上运动时,直接写出![]() 、
、![]() 与
与![]() 之间的数量关系.
之间的数量关系.
【答案】(1)证明见解析;(2)①证明见解析;②![]() .
.
【解析】
(1)根据![]() 易得△BPE 为等边三角形,所以BP=PE,再由速度相同可得BP=CQ,所以EP=CQ;
易得△BPE 为等边三角形,所以BP=PE,再由速度相同可得BP=CQ,所以EP=CQ;
(2)①过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,可证明
,可证明![]() ,可得ED=CD,在等边三角形BPE中,由三线合一可知,F为BE中点,然后可得出
,可得ED=CD,在等边三角形BPE中,由三线合一可知,F为BE中点,然后可得出![]() ;
;
②作PG∥AC交BC的延长线于G,
同理可证明:△PGD≌△QCD,BF=FG
(1)∵![]() 是等边三角形,
是等边三角形,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,![]() .
.
∴![]() 是等边三角形.∴
是等边三角形.∴![]() .
.
∵![]() 、
、![]() 两点运动的速度相同,且同时出发,
两点运动的速度相同,且同时出发,
∴![]() .∴
.∴![]() .
.
(2)①过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,
,
∴![]() ,
,![]() .
.
由(1)得![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() 是等边三角形,
是等边三角形,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
② ![]() . 理由如下:
. 理由如下:
作PG∥AC交BC的延长线于G,
同理可证明:△PGD≌△QCD,BF=FG
∴DC=DG
∴BG-CG=BC,
∴2BF-2CD=BC
即![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某商场第一次用11000元购进某款拼装机器人进行销售,很快销售一空,商家又用24000元第二次购进同款机器人,所购进数量是第一次的2倍,但单价贵了10元.
(1)求该商家第一次购进机器人多少个?
(2)若所有机器人都按相同的标价销售,要求全部销售完毕的利润率不低于20%(不考虑其它因素),那么每个机器人的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 ,∠E=∠F=90°,∠B=∠C,AC=AB,给出下列结论:① ∠1=∠2;② BE=CF;③ △ACN≌△ABM;④ CD=DN,其中正确的结论有( )个

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国西南五省市的部分地区发生严重旱灾,为鼓励节约用水,某市自来水公司采取分段收费标准,右图反映的是每月收取水费y(元)与用水量x(吨)之间的函数关系.
(1)小明家五月份用水8吨,应交水费______ 元;
(2)按上述分段收费标准,小明家三、四月份分别交水费26元和18元,问四月份比三月份节约用水多少吨?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学艺术节期间,学校向学生征集书画作品,杨老师从全校30个班中随机抽取了4个班(用A,B,C,D表示),对征集到的作品的数量进行了分析统计,制作了两幅不完整的统计图.

请根据以上信息,回答下列问题:
(1)杨老师采用的调查方式是 (填“普查”或“抽样调查”);
(2)请你将条形统计图补充完整,并估计全校共征集多少件作品?
(3)如果全校征集的作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生,现要在获得一等奖的作者中选取两人参加表彰座谈会,请你用列表或树状图的方法,求恰好选取的两名学生性别相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步发展基础教育,自2014年以来,某县加大了教育经费的投入,2014年该县投入教育经费6000万元。2016年投入教育经费8640万元。假设该县这两年投入教育经费的年平均增长率相同。
(1)求这两年该县投入教育经费的年平均增长率;
(2)若该县教育经费的投入还将保持相同的年平均增长率,请你预算2017年该县投入教育经费多少万元。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将图1中的正方形剪开得到图2,则图2中共有4个正方形;将图2中的一个正方形剪开得到图3,图3中共有7个正方形;将图3中4个较小的正方形中的一个剪开得到图4,则图4中共有10个正方形,照这个规律剪下去:

(1)根据图中的规律补全表:
图形标号 | 1 | 2 | 3 | 4 | 5 | 6 |
正方形个数 | 1 | 4 | 7 | 10 | _____ | _____ |
(2)第n个图形中有多少个正方形?
(3)当n=673时,图形中有多少个正方形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com