
【题目】如图,已知直线y=![]() x与双曲线y=
x与双曲线y=![]() (k>0)交于A,B两点,且点A的横坐标为4,
(k>0)交于A,B两点,且点A的横坐标为4,

(1)求 k的值;
(2)利用图形直接写出不等式![]() x>
x>![]() 的解;
的解;
(3)过原点O的另一条直线l交双曲线y=![]() (k>0)于P,Q两点(P点在第一象限),若由点 A,B,P,Q为顶点组成的四边形面积为 24,求点 P的坐标.
(k>0)于P,Q两点(P点在第一象限),若由点 A,B,P,Q为顶点组成的四边形面积为 24,求点 P的坐标.
【答案】(1)8;(2)﹣4<x<0和x>4.(3)点P的坐标为(8,1)或(2,4).
【解析】(1)因为点A在直线y=![]() x上,故将其横坐标代入直线的解析式,求出对应的y的值,即可求得点A的坐标,再利用反比例函数图象上点的坐标特征即可求出k值;
x上,故将其横坐标代入直线的解析式,求出对应的y的值,即可求得点A的坐标,再利用反比例函数图象上点的坐标特征即可求出k值;
(2)根据两函数图象的上下位置关系即可得出不等式的解集;
(3)作AM⊥x轴于点M,PN⊥x轴于点N.设P点的坐标为(a,8a),根据正比例函数与反比例函数的对称性即可得出四边形APBQ为平行四边形,结合四边形面积为24以及三角形的面积公式即可得出关于a的一元二次方程,解方程即可得出a值,将其代入点P的坐标中即可得出结论.
(1)∵直线y=![]() x与双曲线y=
x与双曲线y=![]() (k>0)交于A,B两点,且点A的横坐标为 4,
(k>0)交于A,B两点,且点A的横坐标为 4,
∴![]() ×4=2,即:A点的坐标为(4,2),
×4=2,即:A点的坐标为(4,2),
∴k=4×2=8, 即:k的值为 8.
(2)∵点 A与点 B关于原点 O对称,
∴点B的坐标为(﹣4,﹣2),
又∵不等式![]() x>
x>![]() 的解,是函数图象上直线位于双曲线上方的部分对应的x的取值,
的解,是函数图象上直线位于双曲线上方的部分对应的x的取值,
∴由图象可知:不等式 ![]() x>
x>![]() 的解是:﹣4<x<0和x>4.
的解是:﹣4<x<0和x>4.
(3)作AM⊥x轴于点M,PN⊥x轴于点N.设P点的坐标为(a,![]() ).
).
∵P、Q 关于 O 点对称,A、B 关于 O 点对称,
∴四边形 APBQ 为平行四边形,
∴4S△OAP=24
∴S△OAP=6.
①当点 P 在直线 AB 的下方时,如图 1 所示,
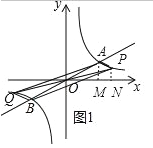
S△OAP=![]() ×4×2+
×4×2+![]() (
(![]() +2)(a﹣4)﹣
+2)(a﹣4)﹣![]() a
a![]() =6,
=6,
∴a2﹣6a﹣16=0,
解得:a1=﹣2,a2=8,
∴此时点P的坐标为(8,1);
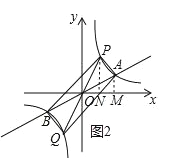
②当点 P 在直线 AB 的上方时,如图 2 所示,
S△OAP=![]() a
a![]() +
+![]() (
(![]() +2)(4﹣a)﹣
+2)(4﹣a)﹣![]() ×4×2=6,
×4×2=6,
∴a2+6a﹣16=0,
解得:a1=2,a2=﹣8,
∴此时点P的坐标为(2,4).
综上所述:点P的坐标为(8,1)或(2,4).


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案科目:初中数学 来源: 题型:
【题目】探究规律
在数轴上,把表示数1的点称为基准点,记作点O.对于两个不同点M和N,若点M和点N到点O的距离相等,则称点M与点N互为基准变换点.例如:图1中MO=NO=2,则点M和点N互为基准变换点.
发现:(1)已知点A表示数a,点B表示数b,点A与点B互为基准变换点.
①若a=0,则b= ;若a=4,则b= ;
②用含a的式子表示b,则b= ;
应用:(2)对点A进行如下操作:先把点A表示的数乘以![]() ,再把所得数表示的点沿着数轴向左移动3个单位长度得到点B.若点A与点B互为基准变换,则点A表示的数是多少?
,再把所得数表示的点沿着数轴向左移动3个单位长度得到点B.若点A与点B互为基准变换,则点A表示的数是多少?
探究:(3)点P是数轴上任意一点,对应的数为m,对P点做如下操作:P点沿数轴向右移动k(k>0)个单位长度得到P1,P2为P1的基准变换点,点P2沿数轴向右移动k个单位长度得到点P3,点P4为P3的基准变换点,“…依次顺序不断的重复,得到P6…,求出数轴上点P2018表示的数是多少?(用含m的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y是x的二次函数,当x=2时,y=﹣4,当y=4时,x恰为方程2x2﹣x﹣8=0的根.
(1)解方程 2x2﹣x﹣8=0
(2)求这个二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点P、Q分别为BC、CD边上一点,且BP=CQ=![]() BC,连接AP、BQ交于点G,在AP的延长线上取一点E,使GE=AG,连接BE、CE.∠CBE的平分线BN交AE于点N,连接DN,若DN=
BC,连接AP、BQ交于点G,在AP的延长线上取一点E,使GE=AG,连接BE、CE.∠CBE的平分线BN交AE于点N,连接DN,若DN=![]() ,则CE的长为_____.
,则CE的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有点a,b,c三点
![]()
(1)用“<”将a,b,c连接起来.
(2)b﹣a 1(填“<”“>”,“=”)
(3)化简|c﹣b|﹣|c﹣a+1|+|a﹣1|
(4)用含a,b的式子表示下列的最小值:
①|x﹣a|+|x﹣b|的最小值为 ;
②|x﹣a|+|x﹣b|+|x+1|的最小值为 ;
③|x﹣a|+|x﹣b|+|x﹣c|的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划从某苗木基地购进A、B两咱树苗共200棵绿化校园。已知购买了3棵A种树苗和5棵B种树苗共需700元;购买2棵A种树苗和1棵B种树苗共需280元.
(1)每棵A种树苗、B种树苗各需多少元?
(2)学校除支付购买树苗的费用外,平均每棵树苗还需支付运输及种植费用20元。设学校购买B种树苗x棵,购买两种树苗及运输、种植所需的总费用为y元,求y与x的函数关系;
(3)在(2)的条件下,若学校用于绿化的总费用在22400元限额内,且购买A种树苗的数量不少于B种树苗的数量,请给出一种费用最省的方案,并求出该方案所需的费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com