
【题目】某单位欲从内部招聘管理人员一名,对甲、乙、丙三名候选人进行了笔试和面试两项测试,三人的测试成绩如下表所示:
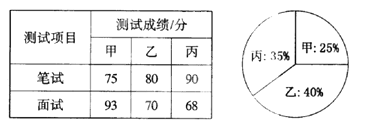
根据录用程序,组织200名职工对三人利用投票推荐的方式进行民主评议,三人得票率(没有弃权票,每位职工只能推荐1人)如扇形图所示,每得一票记作1分.
(l)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用(精确到 0.01 )?
(2)根据实际需要,单位将笔试、面试、民主评议三项测试得分按5 : 2 : 3的比例确定个人成绩,那么谁将被录用?
【答案】(1)候选人乙将被录用;(2)候选人丙将被录用.
【解析】
(1)先根据扇形统计图中的数据即可求得甲、乙、丙的民主评议得分,再根据平均数的概念求得甲、乙、丙的平均成绩,进行比较;
(2)根据加权成绩分别计算三人的个人成绩,进行比较.
解:(l)甲、乙、丙的民主评议得分分别为:甲:200×25%=50 分,
乙:200×40%=80 分,丙:200×35%=70 分.
甲的平均成绩为![]() (分),
(分),
乙的平均成绩为:![]() (分),
(分),
丙的平均成绩![]() (分).
(分).
由于76.67>76>72.67,所以候选人乙将被录用.
(2)如果将笔试、面试、民主评议三项测试得分按5 : 2 : 3的比例确定个人成绩,那么,甲的个人成绩为:![]() (分)
(分)
乙的个人成绩为:![]() (分).
(分).
丙的个人成绩为:![]() (分)
(分)
由于丙的个人成绩最高,所以候选人丙将被录用.


科目:初中数学 来源: 题型:
【题目】在一条平坦的公路旁边建造了A,B两栋住房,这两栋住房与小明所就读的西湖中学在同一条直线上,如图,已知A栋住房有6层,每层高4 m;B栋住房共3层,每层也是4 m,且A,B两栋楼相距30 m,小明家住在A栋楼的第5层,放学后,小明从学校向这两栋楼走来.
问:(1)小明离B栋楼多远时,他才能完全看不到他家的那层楼房?
(2)小明要想完全看到他家的那层楼房,他离B栋楼的距离要满足什么条件(小明的身高不计)?

查看答案和解析>>
科目:初中数学 来源: 题型:
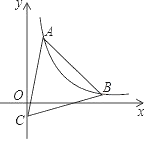
【题目】如图,△ABC是等边三角形,顶点C在y轴的负半轴上,点A(1,![]() ),点B在第一象限,经过点A的反比例函数y=
),点B在第一象限,经过点A的反比例函数y=![]() (x>0)的图象恰好经过顶点B,则△ABC的边长为_____.
(x>0)的图象恰好经过顶点B,则△ABC的边长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先仔细阅读材料,再尝试解决问题:我们在求代数式![]() 的最大或最小值时,通过利用公式
的最大或最小值时,通过利用公式![]() 对式子作如下变形:
对式子作如下变形:
![]() ,
,
因为![]() ,
,
所以![]() ,
,
因此![]() 有最小值2,
有最小值2,
所以,当![]() 时,
时,![]() ,
,![]() 的最小值为2.
的最小值为2.
同理,可以求出![]() 的最大值为7.
的最大值为7.
通过上面阅读,解决下列问题:
(1)填空:代数式![]() 的最小值为______________;代数式
的最小值为______________;代数式![]() 的最大值为______________;
的最大值为______________;
(2)求代数式![]() 的最大或最小值,并写出对应的
的最大或最小值,并写出对应的![]() 的取值;
的取值;
(3)求代数式![]() 的最大或最小值,并写出对应的
的最大或最小值,并写出对应的![]() 、
、![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c (a≠0)的图象如图所示,则①abc>0,②b2-4ac>0,③2a+b>0,④a+b+c<0,这四个式子中正确的个数有( )

A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
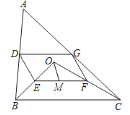
【题目】如图,点![]() 是ΔABC内一点,连接OB、OC,并将AB、OB、OC、AC的中点
是ΔABC内一点,连接OB、OC,并将AB、OB、OC、AC的中点![]() 、
、![]() 、
、![]() 、
、![]() 依次连结,得到四边形
依次连结,得到四边形![]() .
.
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)若![]() 为
为![]() 的中点,OM=5,∠OBC与∠OCB互余,求DG的长度.
的中点,OM=5,∠OBC与∠OCB互余,求DG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
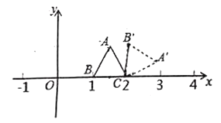
【题目】如图,在平面直角坐标系中,有一个正三角形![]() ,其中
,其中![]() ,
,![]() 的坐标分别为
的坐标分别为![]() 和
和![]() .若在无滑动的情况下,将这个正三角形沿着
.若在无滑动的情况下,将这个正三角形沿着![]() 轴向右滚动,则在滚动过程中,这个正三角形的顶点
轴向右滚动,则在滚动过程中,这个正三角形的顶点![]() ,
,![]() ,
,![]() 中,会过点
中,会过点![]() 的是点__________.
的是点__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
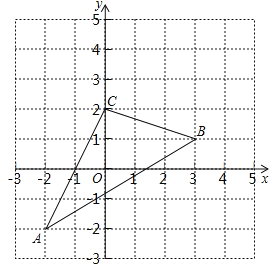
【题目】如图,△ABC在直角坐标系中.
(1)若把△ABC向上平移2个单位,再向左平移1个单位得到△A1B1C1,画出△A1B1C1,并写出点A1,B1,C1的坐标;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进甲、乙两种商品,已知每件甲种商品的价格比每件乙种商品的价格贵10元,用350元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同.
(1)求甲、乙两种商品每件的价格各是多少元?
(2)计划购买这两种商品共50件,且投入的经费不超过3200元,那么最多购买多少件甲种商品?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com