
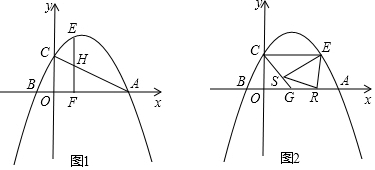
分析 (1)根据待定系数法,可得函数解析式;
(2)根据H是EF的中点,可得关于n的方程,根据解方程,可得答案;
(3)①根据等腰三角形的定义,可得答案;
②根据两边之差小于第三边,可得C,B1,E三点共线,根据线段的和差,可得答案.
解答 解:(1)把A(4,0),B(-1,0)代入y=-$\frac{1}{2}$x2+bx+c得:
$\left\{\begin{array}{l}{-\frac{1}{2}-b+c=0}\\{-\frac{16}{2}+4b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=\frac{3}{2}}\\{c=2}\end{array}\right.$,即:y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2;
(2)求得AC的解析式为y=-$\frac{1}{2}$x+2
设H(n,-$\frac{1}{2}$n+2),由EF⊥x轴,则E(n,-$\frac{1}{2}$n2+$\frac{3}{2}$n+2)
∵EH=FH且点E为抛物线在第一象限上的点,
∴EF=2FH,即-$\frac{1}{2}$n2+$\frac{3}{2}$n+2=2($\frac{1}{2}$n+2)得
n2-5n+4=0,
∴n=1或n=4(舍去)
∴E(1,3);
(3)①设OG=t,则CG=$\sqrt{4+{t}^{2}}$,
∵△COG∽△ESC,
∴$\frac{ES}{CE}$=$\frac{CO}{CG}$,∴$\frac{ES}{3}$=$\frac{2}{\sqrt{4+{t}^{2}}}$
∴ES=$\frac{6}{\sqrt{4+{t}^{2}}}$,
∵∠SER=∠SCE=∠CGO,∴cos∠SER=cos∠CGO=$\frac{t}{\sqrt{4+{t}^{2}}}$.
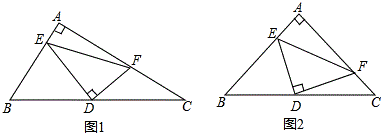
i.如图1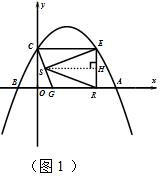 ,
,
当SE=SR时,过点S作SH⊥ER垂足为点H.
∵EH=SE•cos∠SER,
∴1=$\frac{6}{\sqrt{4+{t}^{2}}}$×$\frac{t}{\sqrt{4+{t}^{2}}}$,
∴t=3$±\sqrt{5}$,(t=3+$\sqrt{5}$舍去);
ii.如图2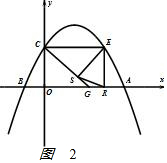 ,
,
当SE=ER时,$\frac{6}{\sqrt{4+{t}^{2}}}$=2,
∴t=$±\sqrt{5}$(t=-$\sqrt{5}$舍去);
iii.如图3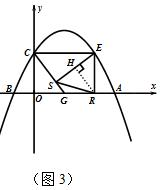 ,
,
当ER=SR时,过点R作RH⊥SE垂足为点H.
∵EH=ER•cos∠SER,
∴$\frac{1}{2}$×$\frac{6}{\sqrt{4+{t}^{2}}}$=2×$\frac{t}{\sqrt{4+{t}^{2}}}$,
∴t=$\frac{3}{2}$;
综上,当△ESR是等腰三角形时OG=3-$\sqrt{5}$或$\sqrt{5}$或$\frac{3}{2}$.
②EB1取最小值时,OG=$\sqrt{5}$-1.
理由如下:如图4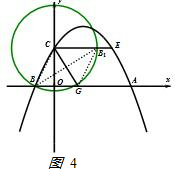 ,
,
CB1=CB,EB1≥CE-CB1=3-$\sqrt{5}$,当点C,B1,E三点共线时,EB1取到最小值,此时四边形CBGB1是菱形,
∴OG=BG-BO=$\sqrt{5}$-1.
点评 本题考查了二次函数综合题,(1)利用待定系数法求函数解析式;(2)利用线段中点的性质是解题关键;(3)领等腰三角形的性质是解题关键,要分类讨论,以防遗漏.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{60}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{12}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 系数是-$\frac{1}{2}$,次数是4 | B. | 系数是-$\frac{1}{2}$,次数是3 | ||
| C. | 系数是-2,次数是4 | D. | 系数是-2,次数是3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
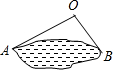 如图所示,为估计池塘岸边A、B的距离,小方在池塘的一侧选取一点O,测得OA=15米,OB=10米,A、B间的距离不可能是( )
如图所示,为估计池塘岸边A、B的距离,小方在池塘的一侧选取一点O,测得OA=15米,OB=10米,A、B间的距离不可能是( )| A. | 5米 | B. | 15米 | C. | 10米 | D. | 20米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com